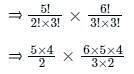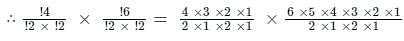Test: Permutations & Combinations - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Permutations & Combinations
Find the sum of all 4-digit numbers that can be formed using 1, 2, 3 and 4 with no digit being repeated in any number.
A committee has 5 men and 6 women. What is the number of ways of selecting 2 men and 3 women from the given committee?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a colony, there are 55 members. Every member posts a greeting card to all the members. How many greeting cards were posted by them?
Find the sum of all four digit numbers that can be formed by the digits 1, 3, 5, 7, 9 without repetition.
Find the number of rectangles and squares in an 8 by 8 chess board respectively.
Number of circular permutations of different things taken all at a time is n!.
How many possible two-digit numbers can be formed by using the digits 3, 5 and 7 (repetition of digits is allowed)?
How many 3 digit odd numbers can be formed from the digits 5, 6, 7, 8, 9, if the digits can be repeated
In how many different ways can the letters of the word 'FIGHT' be arranged?
In how many ways can we sort the letters of the word MANAGEMENT so that the comparative position of vowels and consonants remains the same as in MANAGEMENT.