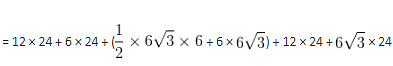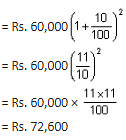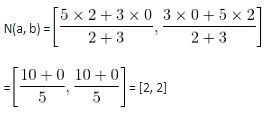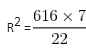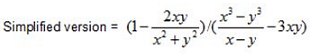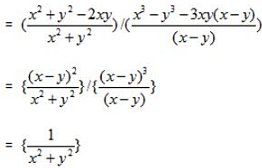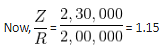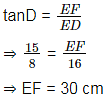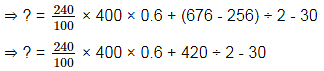SSC CGL (Tier II) Practice Test - 5 - SSC CGL MCQ
30 Questions MCQ Test - SSC CGL (Tier II) Practice Test - 5
If A = 0.abcabc ____, then by which of the following numbers can A be multiplied so as to get an integral value?
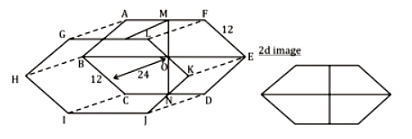
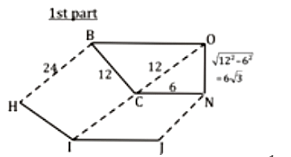
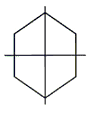
A prism has a regular hexagonal base, whose side is 12 cm. The height of the prism is 24 cm. It is cut into 4 equal parts by 2 perpendicular cuts, as shown in the figure. What is the sum of the total surface area of the four parts?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The wages of three labourers A, B and C are in the ratio 10 : 12 : 15, respectively. A's wage is increased in the ratio 5 : 6, B's wage is increased in the ratio 3 : 4 and C's wage is increased in the ratio 3 : 5. The new ratio of the wages of A, B and C respectively is
In a certain store, the profit is 250% of the cost. If the cost increases by 25%, but the selling price remains constant, then approximately what percentage of selling price is the profit?
For making a colour A, three liquids x, y and z are mixed in the ratio 3 : 5 : 7. For colour B, the ratio is 1 : 8 : 3. If 10 parts of colour A are mixed with 8 parts of colour B, what is the ratio of liquids x, y and z in the resulting mixture?
Work of 2 men is equal to that of 5 women, while the work of 2 women is equal to that of 5 boys. One man alone can complete a job in 120 days. If 4 men, 10 women and 25 boys work together, in how many days would the job be completed?
Avinash borrows Rs. 60,000 from a bank to buy a new machine. If the rate of interest is 10% per annum compounded annually, then what will be the amount payable after two years?
7 years ago, the ages (in years) of A and B were in the ratio 4 : 5 and 7 years hence, they will be in the ratio 5 : 6. The present age of B is
If a point N(a, b) divides the line segment joining the points (0, 0) and (5, 5) internally in the ratio 2 : 3, then the value of b is
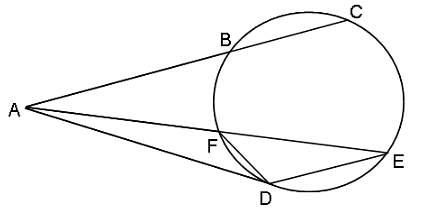
In the figure, if ∠ADF = 25°, AD is a tangent to the circle and DE is parallel to AC, then what is the measure of ∠EAC?
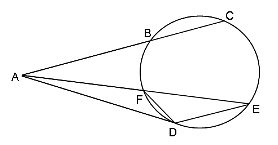
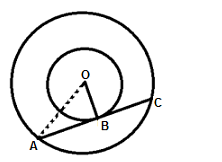
The centre of two concentric circles is O. The areas of the two circles are 616 cm2 and 154 cm2, respectively. A tangent is drawn through point A on the larger circle to the smaller circle. This tangent touches the smaller circle at B and intersects the larger circle at C. What is the length (in cm) of AC?
What is the value of cos (90° - B) sin (C - A) + sin (90° + A) cos (B + C) - sin (90° - C) cos (A + B)?
Directions: Study the following information to answer the question.
The table given below shows the ratio of cars and bikes manufactured by five different companies. The table also shows the ratios of three different types of cars C1, C2 and C3 and three different types of bikes B1, B2 and B3 manufactured by these five different companies. The total numbers of cars and bikes together manufactured by D, E, F, G and H are 3,00,000, 2,80,000, 3,20,000, 4,00,000 and 4,80,000, respectively.
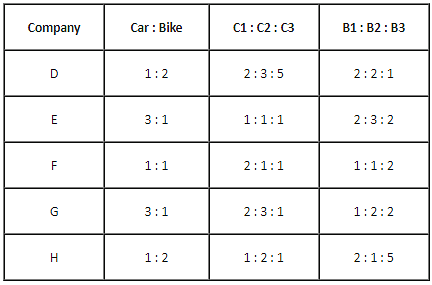
Directions: Study the following information to answer the question.
The table given below shows the ratio of cars and bikes manufactured by five different companies. The table also shows the ratios of three different types of cars C1, C2 and C3 and three different types of bikes B1, B2 and B3 manufactured by these five different companies. The total numbers of cars and bikes together manufactured by D, E, F, G and H are 3,00,000, 2,80,000, 3,20,000, 4,00,000 and 4,80,000, respectively.
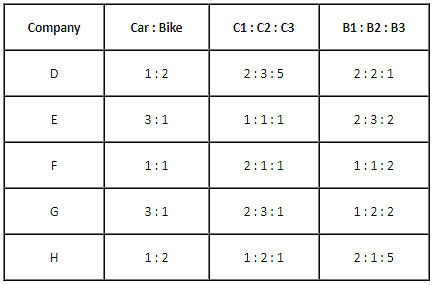
Z = Total number of B2 type bikes manufactured by all the companies
R = Total number of C1 type cars manufactured by companies F, G and D together
What is the value of Z/R?
A trader decided to take loan of Rs. 500000 from XYZ Bank of India at 5% interest rate. He further invests this money and gains 20% return on the money invested such that the difference between total amount after gain and amount to be returned is Rs.75000,then for how many years he took the loan?
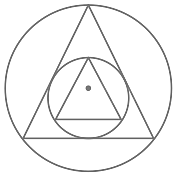
In the given figure find the ratio of sum of inradius and circumradius for smaller triangle and bigger triangle, if the side of smaller equilateral triangle is 25% of the side of bigger equilateral triangle ?
Raman and Tapan starts a business and invested Rs. 10,000 and Rs. 50,000 respectively. After six months Raman added Rs. 10,000 more and Tapan withdrew Rs. 30,000. At the end of the year if business profited Rs. 10,000 then find the profit earned by Tapan.
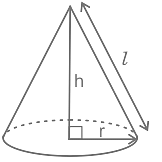
A temple of a conical roof of radius 2 m and height is twice that of the radius. If the cost of painting per sq. m is Rs. 512, then find the total approximate cost of painting the external surface of the conical roof. (in Rs.)
If Vikash walks at the speed of 10 kmph then he misses the bus by 5 min and when he increases his speed to 20 kmph then he reaches the bus station 10 min earlier. Find the distance from Vikash's destination to the bus stop. (in km)
A man sells an article at 10% above its cost price. If he had bought it at 15% less than what he paid for it and sold it for Rs. 33 less, he would have gained 10%. Find the cost price of the article.
Find the compound interest earned in the 9th year, if the compound interest earned on the principal amount Rs. 10000 at the 8th year is Rs. 1948.72 and the rate of interest applied is 10% p.a.
Study the following graph and answer the question given below.
The below Histogram shows the data of the annual rainfall (in cm).
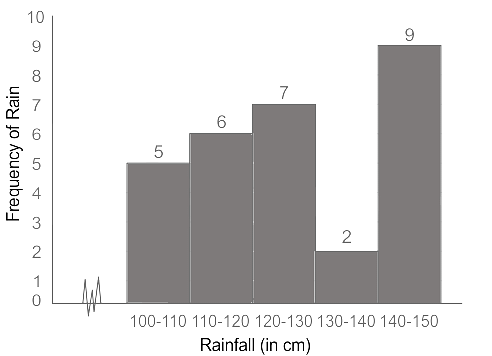
Find the difference in the number of times the rainfall above 130 cm and the number of times the annual rainfall below 130 cm.
Study the below graph and solve the following question.
The below chart shows the percentage wise sale of number of cars on different days.
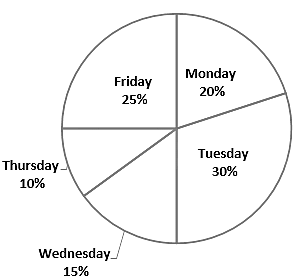
The total number of cars sold = 700
If the total number of cars sold on Saturday is 50% of the total sale of the number of cars on Monday, then find the total number of cars sold on Thursday and Saturday.
Which of the following statement is correct regarding the number 434434?
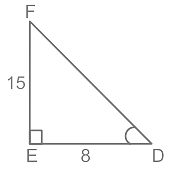
In a ΔDEF where right-angle at E, If tan D = 15/8 and ED = 16 cm, then find the value of EF. (in cm)
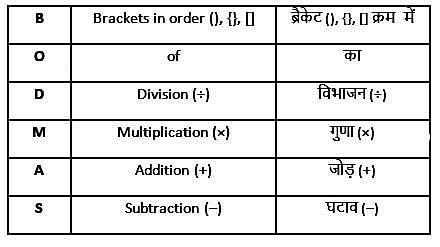
What should come in the place of (?) for the expression given below?
![]()
What should come in the place of (?) for the question given below?
? = 240% of 400 × 0.6 + (262 - 162) ÷ 2 - 30
If (a + b) : (b + c) : (c + a) = 5 : 7 : 8 , Then find the value of ab : bc : ca
What will be the cost of painting the curved surface area of a plastic cylindrical toy with a radius of 42 cm and a height of 3.5 cm? If the cost of painting is at the rate of Rs 70 per cm2.