Test: Joins in Relational Algebra - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Joins in Relational Algebra
Consider two database relations R and S having 3 tuples in R and 2 tuples in S. what is the maximum number of tuples that could appear in the natural join of R and S?
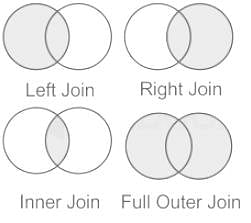
Which of the following Relational Algebra operations can be used when you want to keep all the tuples of the first relation irrespective of whether or not they have matching tuples in the second relation?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
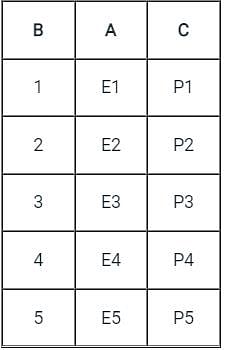
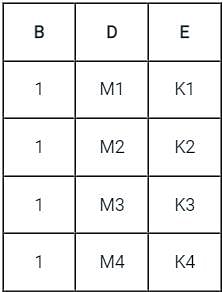
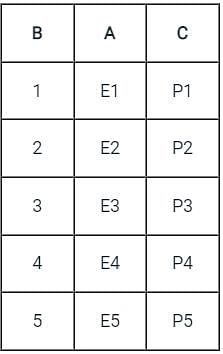
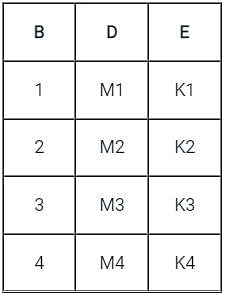
Let the following functional dependencies hold for relation R1(A, B, C) and R2(B, D, E)
B → A, A → C, the relation R1 contains 35 tuples and relation R2 contains 34 tuples. What is maximum number of tuples possible in natural join R1 and R2?
B → A, A → C, the relation R1 contains 35 tuples and relation R2 contains 34 tuples. What is maximum number of tuples possible in natural join R1 and R2?
In relational databases, the natural join of two tables is:
Consider Join of a relation R with a relation S. If R has m tuples and S has n tuples, then maximum and minimum sizes of the Join respectively are
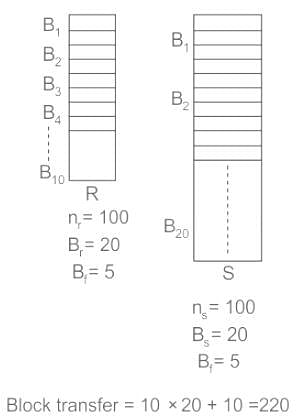
Consider a join (relation algebra) between relations r(R)and s(S) using the nested loop method.
There are 3 buffers each of size equal to disk block size, out of which one buffer is reserved for intermediate results.
Assuming size(r(R))
The following functional dependencies hold for relations R(A, B, C) and S(B, D, E)
B → A,
A → C
The relation R contains 200tuples and the relation S contains 100tuples. What is the maximum number of tuples possible in the natural join R⋈S ?
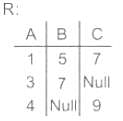
Consider two relations R1(A, B) with the tuples (1, 5), (3, 7) and R2(A, C) = (1, 7), (4, 9). Assume that R(A, B, C) is the full natural outer join of R1 and R2. Consider the following tuples of the form (A, B, C): a = (1, 5, null), b = (1, null, 7), c = (3, null, 9), d = (4, 7, null), e = (1, 5, 7), f = (3, 7, null), g = (4, null, 9). Which one of the following statements is correct?
Consider the relations r(A, B) and s(B, C), where s.B is a primary key and r.B is a foreign key referencing s.B. Consider the query
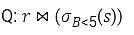
Let LOJ denote the natural left outer-join operation. Assume that r and s contain no null values.
Which one of the following queries is NOT equivalent to Q?


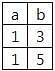
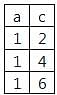
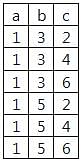
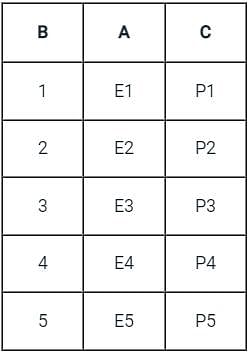
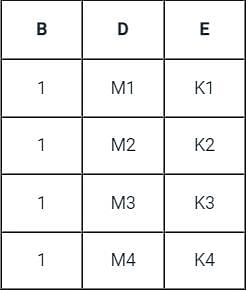
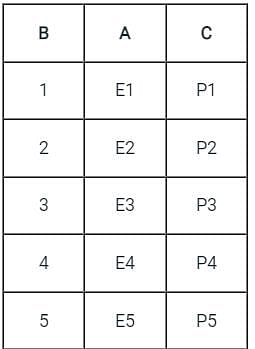
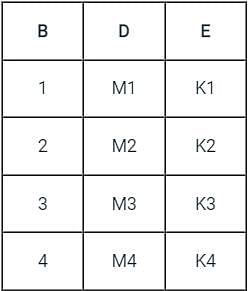
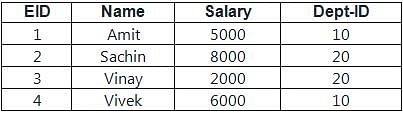

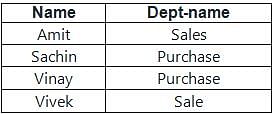
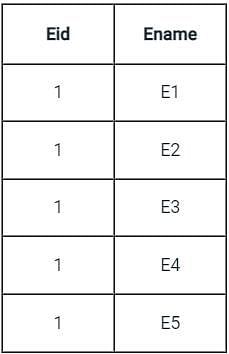

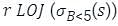 will include record with b > = 5 but other three queries will not.
will include record with b > = 5 but other three queries will not.














