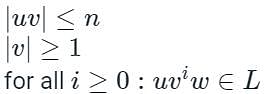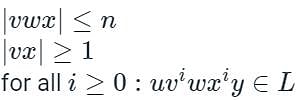Test: Theory of Computation - 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Theory of Computation - 1
Which of the following is sufficient to convert an arbitrary Context Free Grammar (CFG) to an LL(1) grammar?
Which of the following languages accept pumping lemma?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following languages is generated by the given grammar?
S → aS | bS | ϵ
S → aS | bS | ϵ
Identify the language generated by the following grammar, where S is the start variable.
S → XY
X → aX | a
Y → aYb | ϵ
Language L1 is defined by the grammar: S1 → aS1b|ϵ
Language L2 is defined by the grammar: S2 → abS2|ϵ
Consider the following statements:
P: L1 is regular
Q: L2 is regular
Which one of the following is TRUE?
Consider the language L = {an |n ≥ 0} ∪ {anbn| n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
Consider the following statements.
I. If L1 ∪ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
For Σ = {a, b}, let us consider the regular language L = {x|x = a2+3k or x = b10+12k k ≥ 0}.
Which one of the following can be a pumping length (the constant guaranteed by the pumping lemma) for L?
Assume the R is a relation on a set A, aRb is partially ordered such that a and b are _____________
A regular language over an alphabet ∑ is one that cannot be obtained from the basic languages using the operation