Test: Stack - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Stack
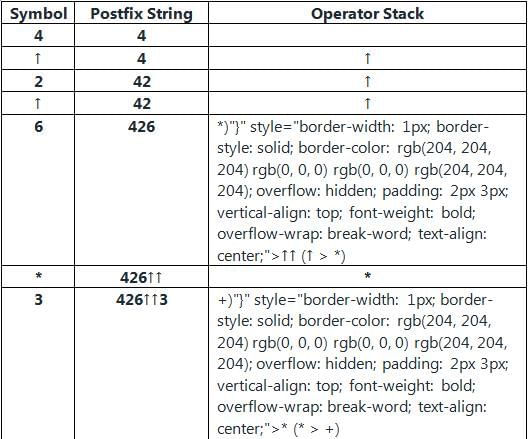
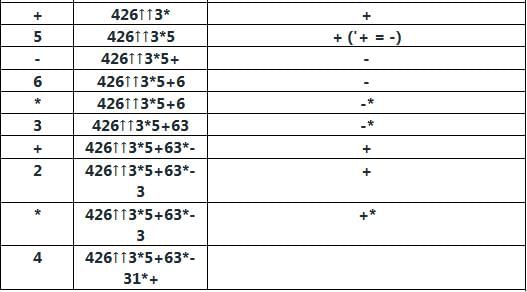
Let there be an infix string given below:
4 ↑ 2 ↑ 6 ∗ 3 + 5 − 6 ∗ 3 + 2 ∗ 4
Assume that the above infix string is being converted in to postfix string. How many maximum memory levels of operand stack will be required for this conversion?
4 ↑ 2 ↑ 6 ∗ 3 + 5 − 6 ∗ 3 + 2 ∗ 4
Assume that the above infix string is being converted in to postfix string. How many maximum memory levels of operand stack will be required for this conversion?
Which of the following data structure to convert an Infix expression into equivalent Prefix/Postfix notation?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
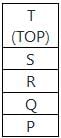
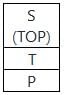
The five items P,Q,R,S and T are pushed in a stack, one after the other starting from P. The stack is popped four times and each element is inserted in a queue. Then two elements are deleted from the queue and pushed back on the stack. now one item is popped from the stack. The popped item is:
A stack is implemented with an array of ‘A [0..N – 1]’ and a variable ‘pos’. The push and pop operations are defined by the following code.
push(x)
A[pos] ← x
pos ← pos – 1
end push
pop( )
pos ← pos + 1
return A[pos]
end pop
Which of the following will initialize an empty stack with capacity N for the above implementation?
If the sequence of operations - push (1), push (2), pop, push (1), push (2), pop, pop, pop, push (2), pop are performed on a stack, the sequence of popped out values
A recursive problem like tower of hanoi can be rewritten without recursion using:
The queue data structure is to be realized by using stack. The number of stacks needed would be
Consider the following pseudo-code to perform push and pop operation on a stack using enqueue(EQ) and dequeue(DQ) operations on 2 queues q1 and q2. Let x be an element to be pushed in the stack. answer the following questions.
push(q1,q2,x)
{
if(q1 is empty)
{
EQ(q2,x);
}
Else
{
EQ(q1,x);
}
}
pop(q1, q2)
{
if (q1 is empty)
{
if (q2 is empty)
{
print “stack underflow”;
Exit;
}
else
{
while(q2 does not contain one element)
{
k= DQ(q2);
EQ(q1,k);
}
Return (DQ(q2));
}
}
Else
{
while(q1 does not contain one element)
{
k= DQ(q1);
EQ(q2,k);
}
Return (DQ(q1));
}
}
If we perform 8 push and 2 pop operations on the above algorithm then total how many enqueue and dequeue operations are performed on queues?
You are given two stacks with the element 1,2,3,4,5, which must be placed in the same sequence in both stacks. Once an element is added to a stack, it can only be popped and displayed (but it cannot be pushed onto the other stack again). So the possible actions are s.pop(), s.push(), and s.top() (to return the stack's top element), and the method display(int) outputs an integer result. Both stacks have access to these three operations. If it is not empty, you can do a pop operation whenever you want. Which of the following sequences cannot be produced with the aforementioned constraints?
What is the postfix representation of the following infix expression?
(A + B) * C – D * E / F
Top Courses for Computer Science Engineering (CSE)
Important Questions for Stack
Stack MCQs with Answers
Online Tests for Stack
|
© EduRev
|
Education Revolution
|
|
