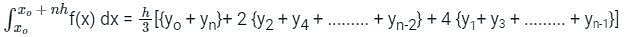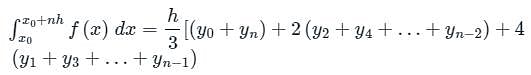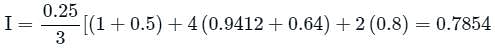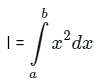Test: Simpson's 1/3rd Rule - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Simpson's 1/3rd Rule
Consider the definite integral 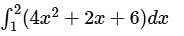 Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
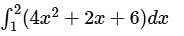 Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e isFind the area of the traverse using Simpson’s rule if d= 12 m and the values of ordinates are 2.25m, 1.46m, 3.23m, 4.46m.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Simpson’s 1/3 rule is used to integrate the function  between x = 0 and x = 1 using the least number of equal sub-intervals. The value of the integral is
between x = 0 and x = 1 using the least number of equal sub-intervals. The value of the integral is
 between x = 0 and x = 1 using the least number of equal sub-intervals. The value of the integral is
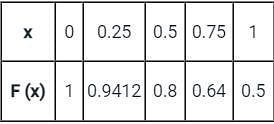
between x = 0 and x = 1 using the least number of equal sub-intervals. The value of the integral isThe table below gives values of function F(x) obtained for values of x at intervals of 0.25.
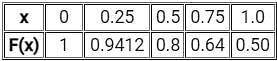
The value of the integral of the function between the limits 0 to 1 using Simpson's rule is
The results obtained are greater than which among the following?
For step-size, Δx = 0.4, the value of the following integral using Simpson’s 1/3 rule is
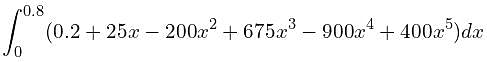
The integral 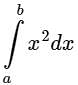 with b > a > 0 is evaluated both analytically and numerically using Simpson's rule with three points. Which of the following relationship is correct ? If I is the exact value of integral obtained analytically and J is the approximate value obtained using Simpson's rule.
with b > a > 0 is evaluated both analytically and numerically using Simpson's rule with three points. Which of the following relationship is correct ? If I is the exact value of integral obtained analytically and J is the approximate value obtained using Simpson's rule.
Find the area of segment if the values of co-ordinates are given as 119.65m, 45.76m and 32.87m. They are placed at a distance of 2 m each.
The magnitude of the error (correct to two decimal places) in the estimation of following integral using Simpson’s 1/3 rule. Take the step length as 1

In which of the following cases, Simpson’s rule is adopted?