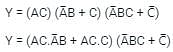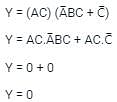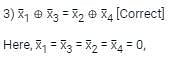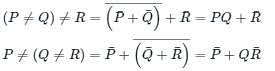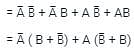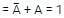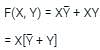Test: Boolean logic - Humanities/Arts MCQ
15 Questions MCQ Test - Test: Boolean logic
Which of the is sufficient to represent any boolean operation.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let A, B, C, and D be boolean variables. Choose the correct options that is/are not equivalent to the boolean expression given below.
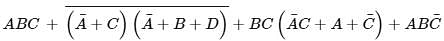
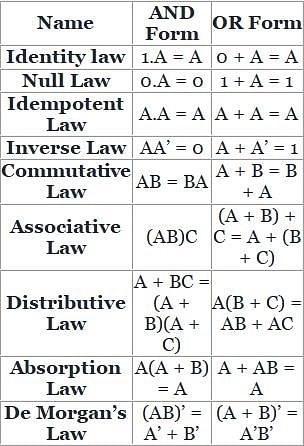
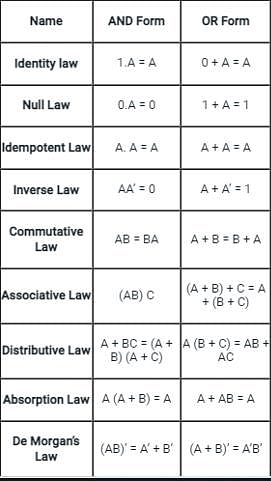
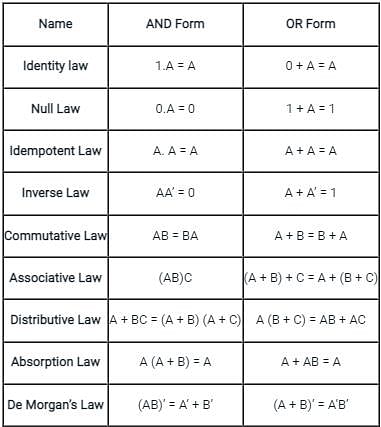
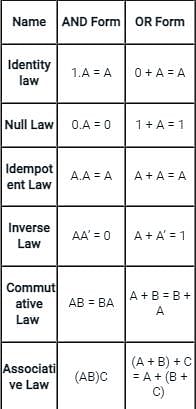
Match the following identities/laws to their corresponding name:

Solve the following Boolean expression:
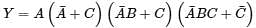
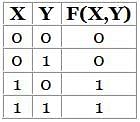
Select the correct option.
Let, x1 ⊕ x2 ⊕ x3 ⊕ x4 = 0 where x1, x2, x3, x4 are Boolean variables, and ⊕ is the XOR operator.
Which one of the following must always is TRUE?
Let # be a binary operator defined as
X # Y = X’ + Y’ where X and Y are Boolean variables.
Consider the following two statements.
(S1) (P # Q) #R = P# (Q # R)
(S2) Q # R = R # Q
Which of the following is/are true for the Boolean variables P, Q and R?
If function f(A, B) = ∑ m(0, 1, 2, 3) is implemented using SOP form, the resultant Boolean function would be:


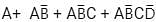 simplifies to:
simplifies to: 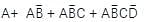
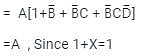
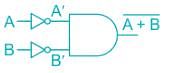
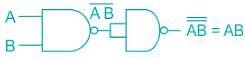
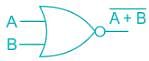
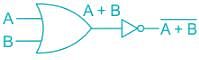
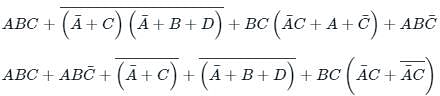
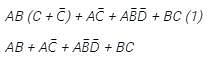
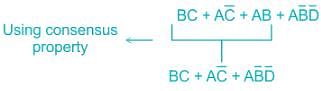
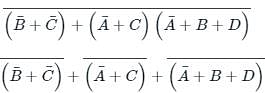
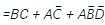
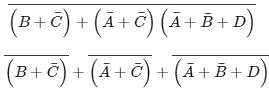
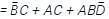
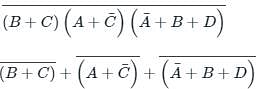
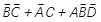
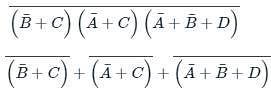
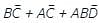
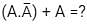
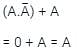
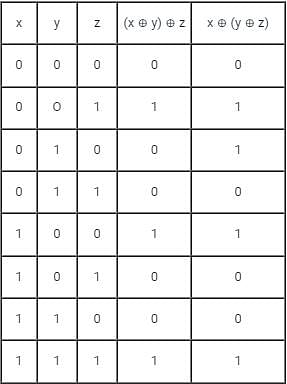
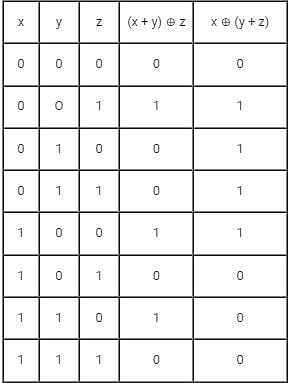
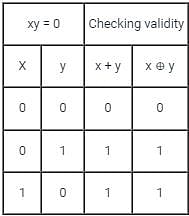
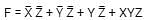
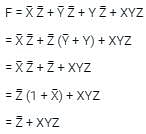
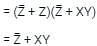

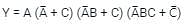
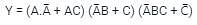
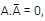 the above expression can be written as:
the above expression can be written as: