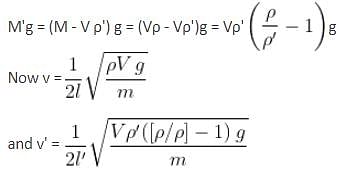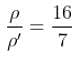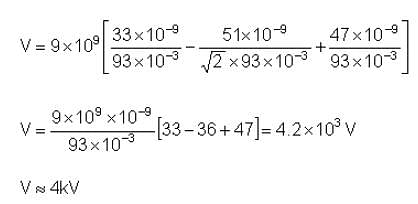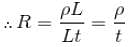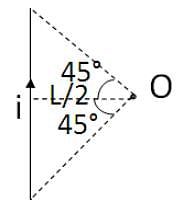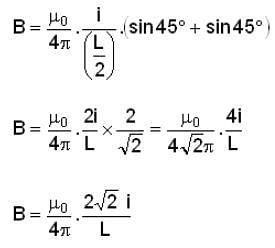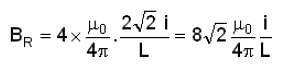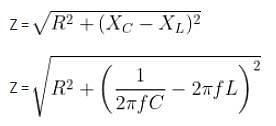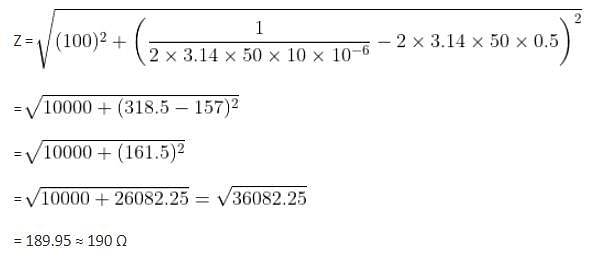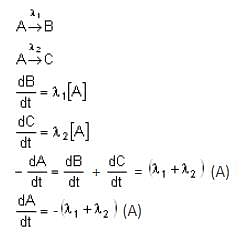BITSAT Practice Test - 7 - JEE MCQ
30 Questions MCQ Test - BITSAT Practice Test - 7
A particle begins to move with a tangential acceleration of constant magnitude 0.6ms-2 in a circular path. If it slips when its total acceleration becomes 1 ms−2, then the angle through which it would have turned before it started to slip is
A solid sphere rolls down without slipping on an inclined plane at angle 60° over a distance of 10 m. The acceleration (in m s−2) is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A cube has a side of length 1.2 x10-2m. Calculate its volume.
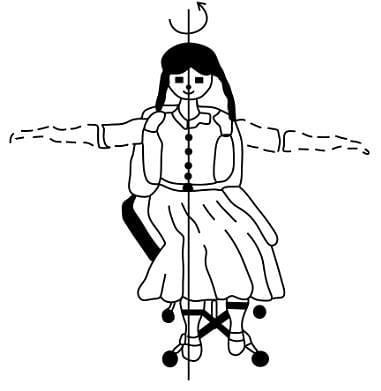
If frictional force is neglected and girl bends her hand, then (initially girl is rotating on chair)
A particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2Rt2, where n is a constant. The power delivered to the particle by the force acting on it, is :
If a piece of metal is heated to temperature θ and then allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closest to :
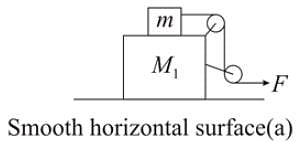
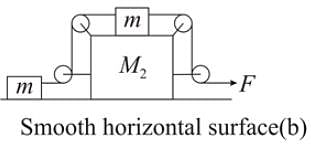
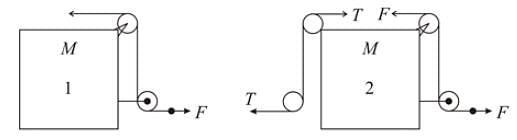
In the situation shown in figure all the strings are light and inextensible and pulleys are light. There is no friction at any surface and all block are of cuboidal shape. A horizontal force of magnitude F is applied to right most free end of string in both cases of figure 1 and figure 2 as shown. At the instant shown, the tension in all strings are non zero. Let the magnitude of acceleration of large blocks (of mass M) in figure 1 and figure 2 are a1 and a2 respectively. Then :
Two spherical bodies of the same mass M are moving with velocities v1 and v2 . These collide perfectly inelastically. What is the loss in kinetic energy
A pipe open at both the ends produce a note of fundamental frequency v1. When the pipe is kept with (3/4)th of its length in water, it produces a note of fundamental frequency v2. The ratio of v1/v2 is
In Young's double-slit experiment, the distance between slits is d/3 and the distance between screen and slits is 3D, then fringe width is
A beam of light of wavelength 400 nm and power 1.55 mW is directed at the cathode of a photoelectric cell. If only 10% of the incident photons effectively produce photoelectrons, then find current due to these electrons.
(given, hc=1240eV -nm, e= 1.6x10-19C
In an experiment, a boy plots a graph between (vmax)2 and (amax)2 for a simple pendulum for different values of (small) amplitudes, where vmax and amax is the maximum velocity and the maximum acceleration respectively. He found the graph to be a straight line with a negative slope, making an angle of 30° when the experiment was conducted on the earth surface. When the same experiment was conducted at a height h above the surface, the line was at an angle of 60°. The value of h is [radius of the earth = R]
If a vector  is perpendicular to the vector
is perpendicular to the vector  then the value of α is
then the value of α is
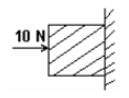
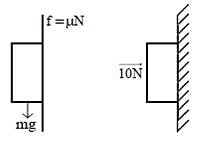
A horizontal force of 10 N is necessary to just hold a stationary block against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
Spheres A and B of equal radius and of masses 2 m and m, respectively, are moving towards each other and strike directly. The speeds of A and B before the collision are 3u and u, respectively. The collision is such that B experiences an impulse of 4mcu, where c is constant.
What is the coefficient of restitution?
A body is projected vertically upward from the surface of the Earth with a velocity equal to half the escape velocity. If R is the radius of the Earth, then the maximum height attained by the body is
If a wire having initial diameter of 2 mm produces the longitudinal strain of 0.1%, then the final diameter of wire is
(σ = 0.5)
A point particle of mass 0.1 kg is executing SHM of amplitude 0.1 m. When the particle passes through the mean position, its KE is 8 x 10-3 J. What is the equation of motion of this particle if the initial phase of oscillation is 45o?
A stone hangs from the free end of a sonometer wire whose vibrating length, when tuned to a tuning fork, is 40 cm. When the stone hangs wholly immersed in water, the resonant length is reduced to 30 cm. The relative density of the stone is
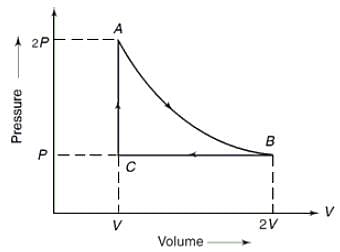
The figure below shows the P - V diagram for a fixed mass of an ideal gas undergoing cyclic process ABCA. If the temperature at A is T, then what is the temperature at C?
The potential at a point P, which is forming a corner of a square of side 93 mm with charges q1 = 33 nC, q2 = -51 nC and q3 = 47 nC located at the other three corners is nearly
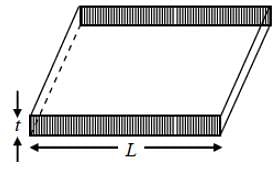
Consider a thin square sheet of side L and thickness t, made of a material of resistivity ρ. The resistance between two opposite faces shown by the shaded areas in the figure is
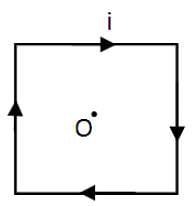
A square wire of each side L carries a current i. What is the magnetic field at the mid-point of the square?
If a resistance of 100 Ω, an inductance of 0.5 H and a capacitance of 10 x 10−6 F are connected in series with a 50 Hz AC supply, then what will be the impedance?
In a single-slit diffraction experiment, the width of the slit is made double its original width. The central maximum of the diffraction pattern will become
Assuming human pupil to have a radius of 0.25 cm and a comfortable viewing distance of 25 cm, the minimum separation between two objects that human eye can resolve at 500 nm wavelength is
A radioactive nuclide can decay simultaneously by two different processes, which have individual decay constants and λ2, respectively. The effective decay constant of the nuclide is given by


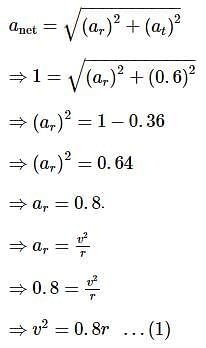


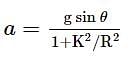

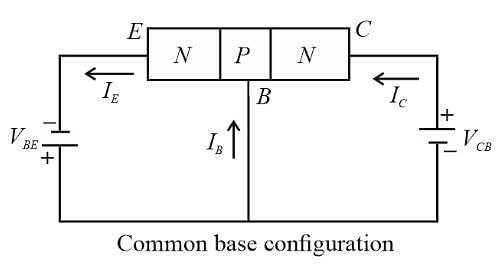
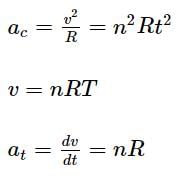


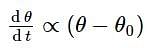
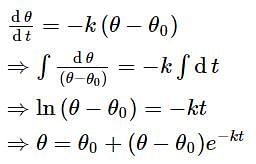
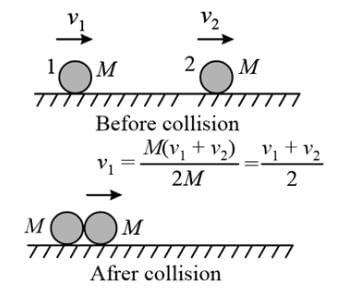
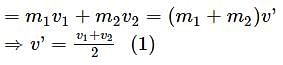

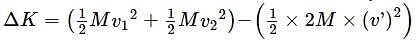
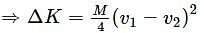
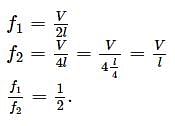
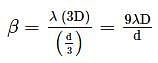
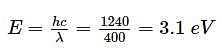
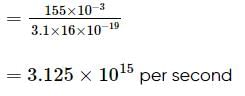
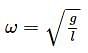
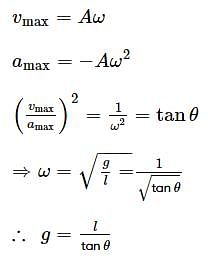
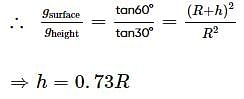
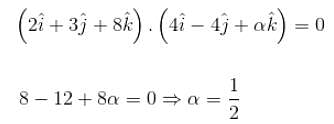
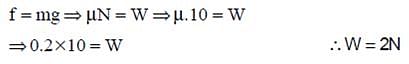


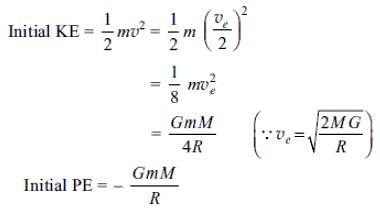
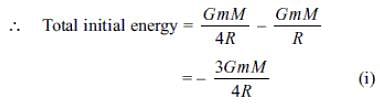
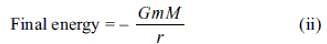
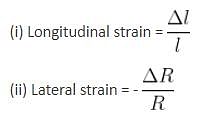


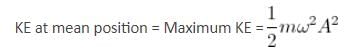
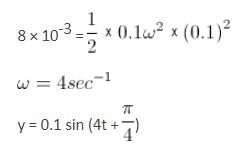
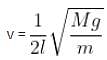 where M = mass of stone. If ρ is the density of the stone and V its volume, then m = ρV.
where M = mass of stone. If ρ is the density of the stone and V its volume, then m = ρV.