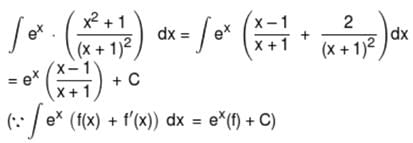BITSAT Practice Test - 10 - JEE MCQ
30 Questions MCQ Test - BITSAT Practice Test - 10
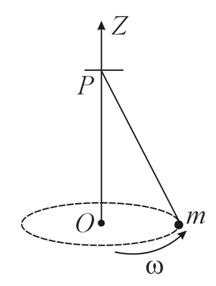
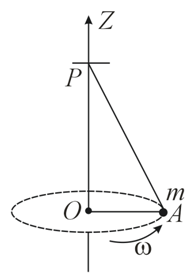
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion is the x − y plane with centre at O and constant angular speed ω. If the angular momentum of the system, calculated about O and P are denoted by  , respectively, then
, respectively, then
 , respectively, then
, respectively, then
If the velocity of a particle is 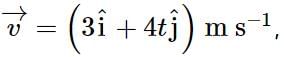 find the acceleration of the particle at t = 1 s.
find the acceleration of the particle at t = 1 s.
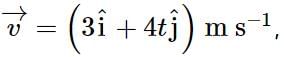 find the acceleration of the particle at t = 1 s.
find the acceleration of the particle at t = 1 s.Two pendulums begin to swing simultaneously. If the ratio of the frequency of oscillations of the two is 7 : 8, then the ratio of lengths of the two pendulums will be
Efficiency of a carnot engine is 50% when temperature of outlet is 500 K. In order to increase its efficiency up to 60%, keeping temperature of intake the same, what should be the temperature of outlet?
If the radii of circular paths of two particles of same masses are in the ratio of 1 : 2, then in order to have same centripetal force, their speeds should be in the ratio of:
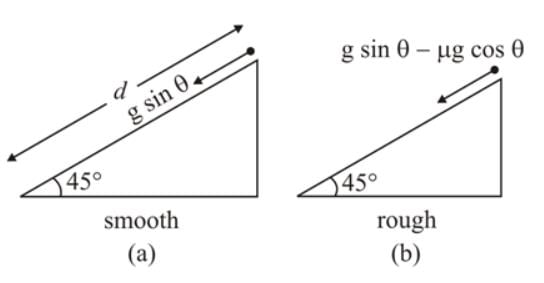
A smooth block is released from rest on a 45° incline and then, it slides a distance d. The time taken to slide is n times as much to slide on a rough incline than on a smooth incline. The coefficient of friction is,
A current-carrying coil is subjected to a uniform magnetic field. The coil will orient so that its plane becomes
A radioactive material decays by simultaneous emission of two particles with half-lives 1620 years and 810 years respectively. The time in years after which one-fourth of material remains, is
The emf of a standard cell is 1.5 V and its balancing length is 7.5 m. The balancing length (in meters) for a 3.5 Ω resistance, through which a current of 0.2 A flows will be
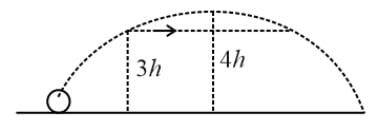
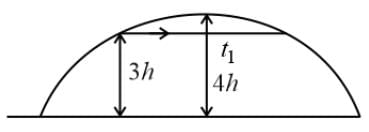
A stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10 m s−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
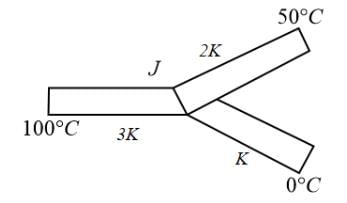
Three rods of same dimensions have thermal conductivities 3K, 2K and K, with their ends at 100°C, 50°C and 0°C respectively. They are arranged as shown in the diagram. The temperature of the junction J in steady-state is:
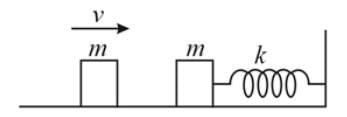
In the figure given below, the mass on the left is moving to the right with a constant velocity v and after colliding inelastically with the mass on the right, sticks to it. If the spring of spring constant k was initially at its equilibrium position, what is the amplitude to the resultant oscillation?
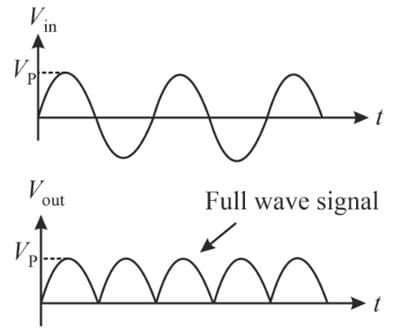
In a full-wave rectifier, circuit operating from 60 Hz main frequency, the fundamental frequency in ripple would be,
The potentiometer wire 10 m long and 20 Ω resistance is connected to a 3 V emf battery and a 10 Ω resistance. The value of potential gradient in V m−1 of the wire will be
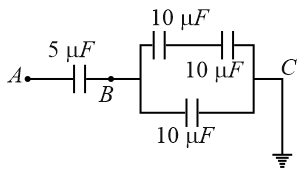
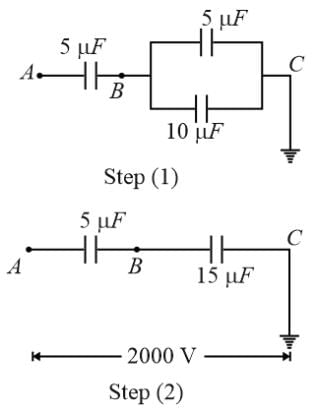
In the given circuit, if point C is connected to the earth and a potential of +2000 V is given to the point A, the potential at B is
A parachutist, after bailing out, falls 50 m without friction. When parachute opens, it retards at 2 ms-2. He reaches the ground with a speed of 3 ms-1. At what height did he bail out?
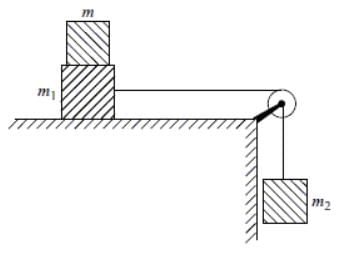
Two blocks of masses m1 = 4 kg and m2 = 6 kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure. The coefficient of friction between block m1 and the horizontal surface is 0.4. When the system is released, the masses m1 and m2 start accelerating. What additional mass m should be placed over mass m1 so that the masses (m1 + m) slide with a uniform speed?
A spring scale is adjusted to read zero. Particles of mass 1 g fall on the pan of the scale and collide elastically and they rebound upward with the same speed. If the height of fall of particles is 2 metres and their rate of collision is 100 particles per second, then the scale reading (in grams) will be
The potential energy of a 1 kg particle, free to move along the x-axis, is given by V(x) = J. The total mechanical energy of the particle is 2 J. Then, the maximum speed (in m/s) is
A rocket is fired from Earth to the Moon. The distance between Earth and the Moon is r and the mass of Earth is 81 times the mass of the Moon. The gravitational force on the rocket will be zero when its distance from the Moon is
When water flows at a rate Q through a capillary tube of radius r that is placed horizontally, a pressure difference p develops across the ends of the tube. If the radius of the tube is doubled and the rate of flow halved, the pressure difference becomes
A uniform rope of length 12 m and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced in the lower end of the rope. What is the wavelength of the pulse, when it reaches the top of the rope?
The electric potential V (in volts) varies with x (in metres) according to the relation V = 5 + 4x2. The force experienced by a negative charge of 2 x 10-6 C, located at x = 0.5 m, is
A metallic sphere A of radius 'a' carries a charge Q. It is brought in contact with an uncharged sphere B of radius 'b'. The charge on sphere A now will be
The resistance of a coil is 4.2 Ω at 100oC and the temperature coefficient of resistance of its material is 0.004oC. Its resistance will be 4 Ω at
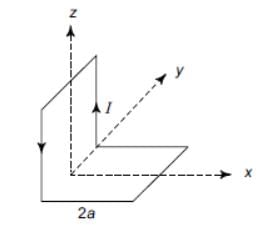
A non-planar loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P (a, 0, a) points in the direction
Two particles, each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2I. The rod is rotated at a constant angular speed about a perpendicular axis that passes through its centre. The ratio of the magnitude of the magnetic moment of the system to its angular momentum about the centre of the rod is
When one of the slits in Young's experiment is covered with a transparent sheet of thickness 3.6 x 10-3 cm, the central fringe shifts to a position originally occupied by the 30th bright fringe. If λ = 6000 Å, then the refractive index of the sheet is
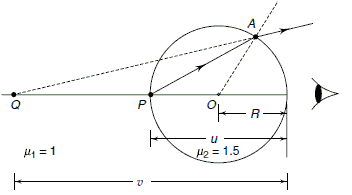
A mark is made on the surface of a glass sphere of diameter 10 cm and refractive index 1.5. It is viewed through the glass from a portion directly opposite. The distance of the image of the mark from the centre of the sphere will be


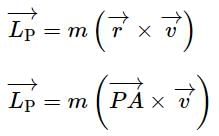
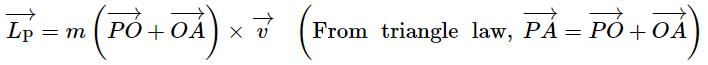
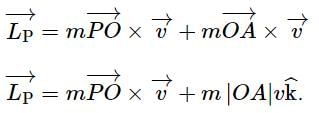
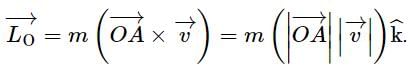
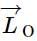 is constant.
is constant.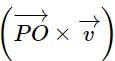 will continuously change its direction.
will continuously change its direction. will change its direction at every instant and thus varies.
will change its direction at every instant and thus varies.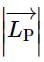 = constant.
= constant.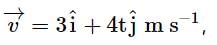
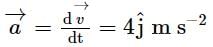

 now if the acceleration due to gravity is g.
now if the acceleration due to gravity is g.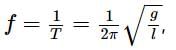
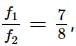 it means,
it means,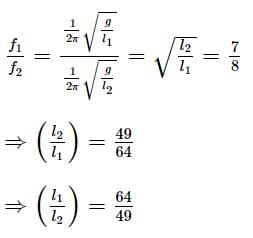
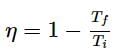
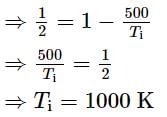
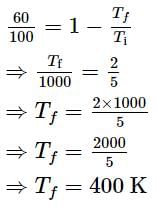
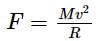 acting towards the centre along the radius. In the following diagram, according to the question,
acting towards the centre along the radius. In the following diagram, according to the question,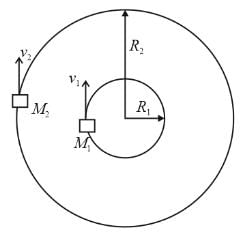
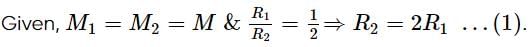 Centripetal forces are the same, so,
Centripetal forces are the same, so, 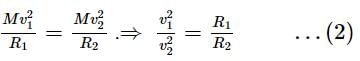
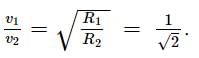
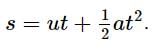

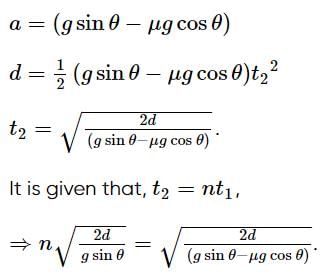
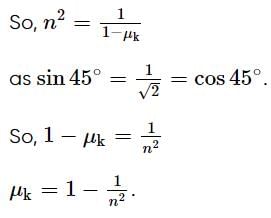
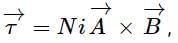 so torque will be zero when area vector
so torque will be zero when area vector  is parallel to magnetic field
is parallel to magnetic field  i.e. when the plane of the coil is perpendicular to the magnetic field. This is so because area vector is perpendicular to the plane of the loop.
i.e. when the plane of the coil is perpendicular to the magnetic field. This is so because area vector is perpendicular to the plane of the loop.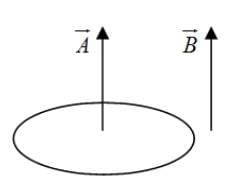
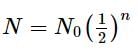
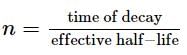
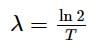
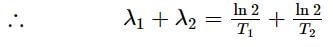
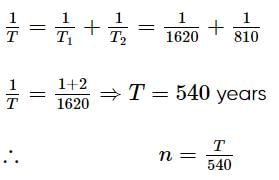
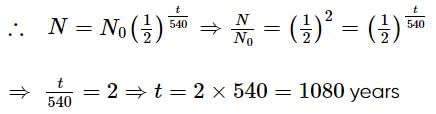
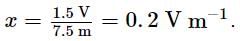
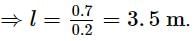
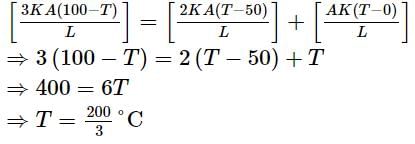
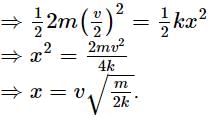
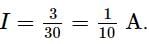
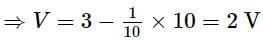
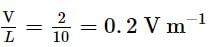
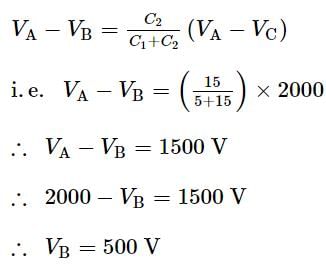
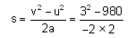
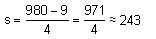
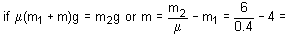 11 kg
11 kg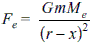
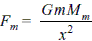
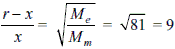
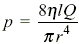
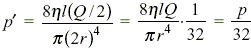
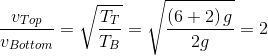
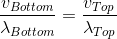


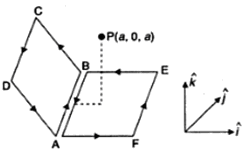
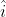 and due to loop AFEBA, along
and due to loop AFEBA, along 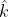 .
.
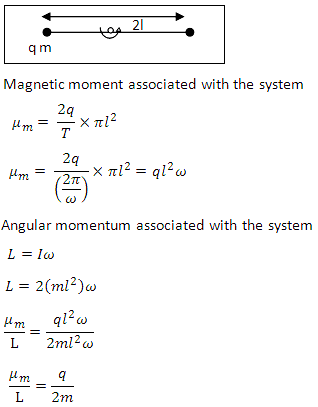

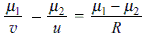
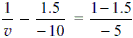
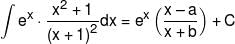 then value of (a + b) = ?
then value of (a + b) = ?