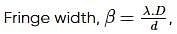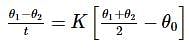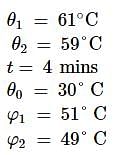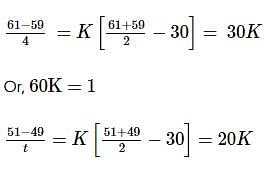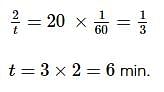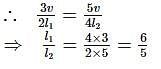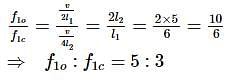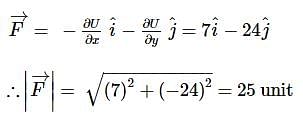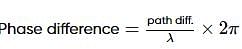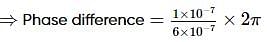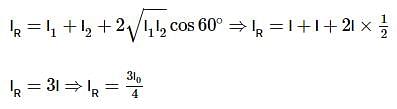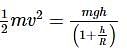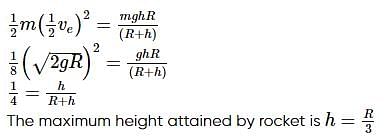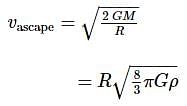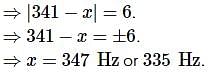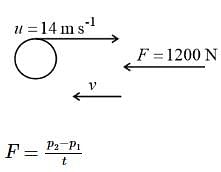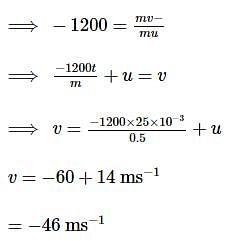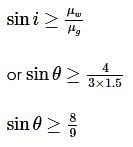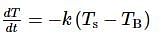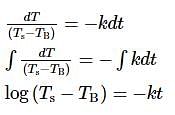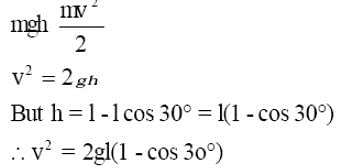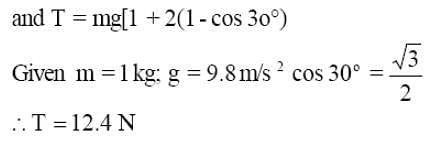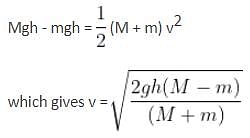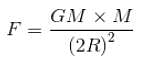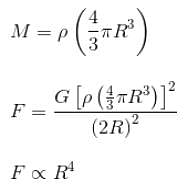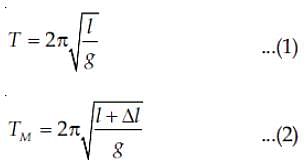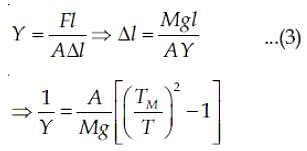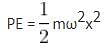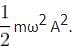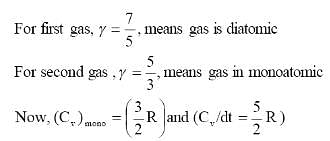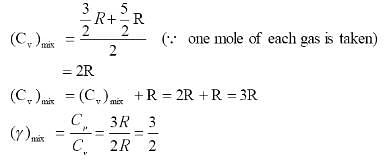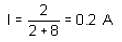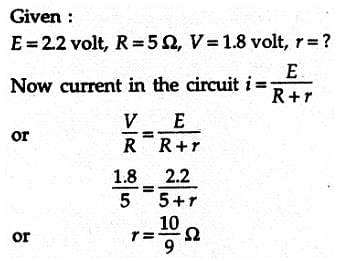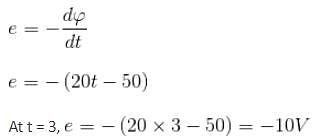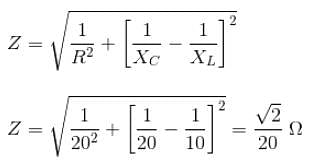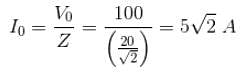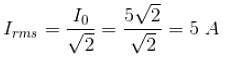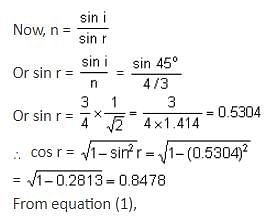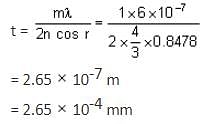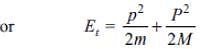BITSAT Practice Test - 13 - JEE MCQ
30 Questions MCQ Test - BITSAT Practice Test - 13
If the source of light used in a Young's double slit experiment is changed from red to violet,
A body in laboratory takes 4 minutes to cool from 61℃ to 59℃. If the laboratory temperature is 30℃, then the time taken by it to cool from 51℃ to 49℃ is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The second overtone of an open pipe A and a closed pipe B have the same frequencies at a given temperature. Both the pipes contain air. The ratio of fundamental frequency of A to that of B is,
A particle of mass 5 kg moving in the x−y plane has its potential energy given by U = (−7x+24y) Joule, x and y
being in meter. Initially at t =0 ,the particle is located at the origin (0, 0) and moving with a velocity of 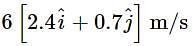 . Find the magnitude of force acting on the particle.
. Find the magnitude of force acting on the particle.
In a double-slit experiment, the separation between the slits is d=0.25 cm and the distance of the screen D=100 cm from the slits. If the wavelength of light used is 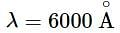 and I0 is the intensity of the central bright fringe, the intensity at a distance x=4 x 10−5 m from central maximum is
and I0 is the intensity of the central bright fringe, the intensity at a distance x=4 x 10−5 m from central maximum is
A rocket is fired perpendicular to the surface of the earth with a speed equal to 50% of the escape velocity from earth surface. The maximum height reached by it in terms of radius R of the earth is :
The escape velocity from the earth is 11 km s−1. The escape velocity from a planet having twice the radius and same mean density as that of the earth is
In Bernoulli's theorem, which of the following is conserved?
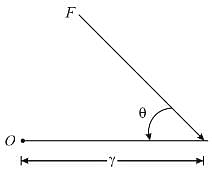
The vector product of the force (F) and distance (r) from the centre of action represents
When a tuning fork of frequency 341 Hz is sounded with another tuning fork, six beats per second are heard. When the second tuning fork is loaded with wax and sounded with the first tuning fork, the number of beats is two per second. The natural frequency of the second tuning fork is
A force of 1200 N acts on a 0.5 kg steel ball as result of collision lasting 25 ms. If the force is in a direction opposite to the initial velocity of 14 ms then the final speed of the steel ball would be
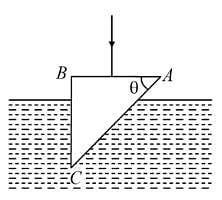
Figure shows, a glass prism ABC (refractive index 1.5), immersed in water (refractive index 43). A ray of light incident normally on face AB. If it is totally reflected at face AC then
A hot liquid is kept in a big room. The logarithm of the numerical value of the temperature difference between the liquid and the room is plotted against time. The plot will be very nearly,
Three identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at a separation of 10 m
between them as shown in the figure. Initially, the balls are stationary. Ball I is given a velocity of 10 m s−1 towards ball II. The collision between ball I and II is inelastic with coefficient of restitution 0.5 but collision between ball II
and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II ?

A semiconductor has an electron concentration of 8×1013 per cm3 and a hole concentration of 5 x 1012 per cm3. The electron mobility is 25000 cm2 V−1 s−1
and the hole mobility is 100 cm2 V. s−1 . Then,
A particle moves in xy plane according to the law x = a sin ωt and y = a(1 - cos ωt), where a and w are constant. The particle traces
In the given figure, the block of mass M is at rest on the floor. The acceleration with which a boy of mass m should climb along the rope of negligible mass so as to lift the block from the floor, is

A uniform metal chain is placed on a rough table, such that one end of it hangs down over the edge of the table. When one-third of its length hangs over the edge, the chain starts sliding. Then, the coefficient of static friction is
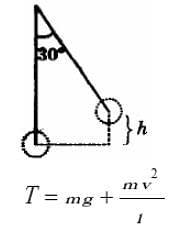
A mass of 1 kg suspended by a thread deviates through an angle of 30°. Find the tension of the thread at the moment the weight passes through the position of equilibrium?
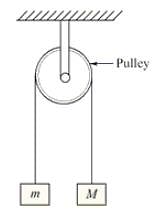
Two masses M and m (with M > m) are connected by means of a pulley as shown in the figure. The system is released. At the instant when mass M has fallen through a distance h, the velocity of mass m will be
Two identical solid copper spheres of radius R are placed in contact with each other. The gravitational attraction between them is proportional to
A pendulum made of a uniform wire of cross-sectional area A has time period T. When an additional mass M is added to its bob, the time period changes to TM. If the Young's modulus of the material of the wire is Y, then 1/Y is equal to
(g = gravitational acceleration)
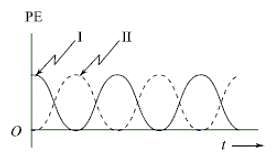
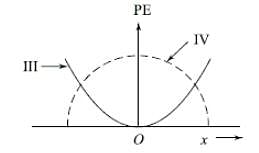
For a particle executing simple harmonic motion, the displacement x is given by x = A cosωt. Identify the graphs which represent the variation of potential energy (PE) as a function of time t and displacement x (see figure).
1 mole of a gas with γ = 7/5 is mixed with 1 mole of a gas with γ = 5/3, then the value of γ for the resulting mixture is
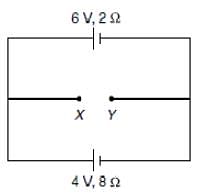
The figure below shows a circuit with two cells in opposition to each other. One cell has an emf of 6 V and internal resistance of 2Ω and the other cell has an emf of 4 V and internal resistance of 8Ω. The potential difference across the terminals X and Y is
The potential difference between the terminals of a cell in open circuit is 2.2 volt with resistance of 5 ohm across the terminals of a cell, the terminal potential difference is 1.8 volt. The internal resistance of the cell is
The flux linked with a coil at any instant t is given by
φ = 10t2 - 50t + 250
The induced emf at t = 3 s is
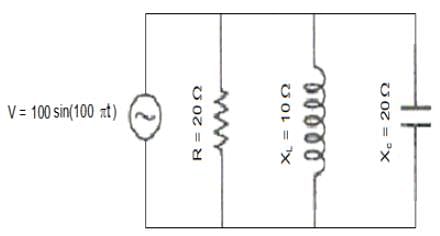
In the given circuit, the current drawn from the source is
A soap film of refractive index 4/3 is illuminated by white light incident at an angle of 45°. The transmitted light is examined in a spectroscope and a bright band is found to be at 6000 . Find the thickness of the film.
. Find the thickness of the film.
A radioactive element of mass number 208 at rest disintegrates by emitting an α-particle. If E is the energy of the emitted α-particle, then the energy of disintegration is