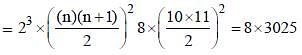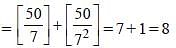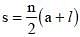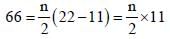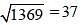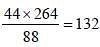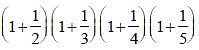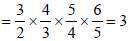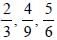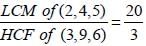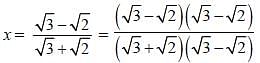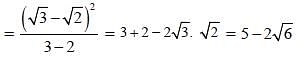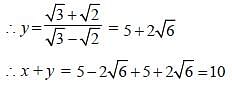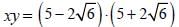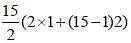SSC CGL Previous Year Questions: Number System and HCF & LCM- 2 - SSC CGL MCQ
30 Questions MCQ Test - SSC CGL Previous Year Questions: Number System and HCF & LCM- 2
If X and Y are the two digits of the number 347XY such that the number is completely divisible by 80, then what is the value of X + Y? (SSC CGL 2017)
What least value must be assigned to '*' so that the numbers 451*603 is exactly divisible by 9? (SSC CGL 1st Sit. 2016)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
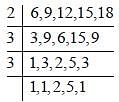
The least number which when divided by 6, 9, 12, 15, 18 leaves the same remainder 2 in each case is: (SSC CGL 2nd Sit. 2015)
The least number that should be added to 2055 so that the sum is exactly divisible by 27 : (SSC CGL 1st Sit. 2015)
If 13 + 23 + ..... + 103 – 3025, then the value of 23 + 43 +..... + 203 is : (SSC CHSL 2015)
The smallest five digit number which is divisible by 12, 18 and 21 is : (SSC CHSL 2015)
If the product of first fifty positive consecutive integers be divisible by 7n, where n is an integer, then the largest possible value of n is (SSC CGL 1st Sit. 2014)
The first term of an Arithmetic Progression is 22 and the last term is –11. If the sum is 66, the number of terms in the sequence are : (SSC CHSL 2014)
A teacher wants to arrange his students in an equal number of rows and columns. If there are 1369 students, the number of students in the last row are (SSC CHSL 2014)
The H.C.F. and L.C.M. of two numbers are 44 and 264 respectively. If the first number is divided by 2, the quotient is 44. The other number is (SSC CHSL 2014)
Three tankers contain 403 litres, 434 litres, 465 litres of diesel respectively. Then the maximum capacity of a container that can measure the diesel of the three container exact number of times is (SSC Sub. Ins. 2014)
The next term of the sequence, 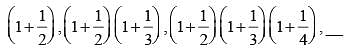 is (SSC Sub. Ins. 2014)
is (SSC Sub. Ins. 2014)
Find the number lying between 900 and 1000 which when divided by 38 and 57 leaves in each case a remainder 23. (SSC Multitasking 2014)
The sum of the squares of the digits of the largest prime number in two digits is (SSC Multitasking 2014)
A number x when divided by 289 leaves 18 as the remainder. The same number when divided by 17 leaves y as a remainder. The value of y is (SSC CGL 2nd Sit. 2013)
Product of two co-prime numbers is 117. Then their L.C.M. is (SSC CGL 2013)
The fifth term of the sequence for which t1 = 1, t2 = 2 and tn + 2 = tn + tn + 1, is (SSC CGL 1st Sit. 2013)
If the sum of the digits of any integer lying between 100 and 1000 is subtracted from the number, the result always is (SSC CHSL 2013)
'a' divides 228 leaving a remainder 18. The biggest two-digit value of ‘a’ is (SSC CHSL 2013)
L.C.M. of 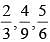 is (SSC CHSL 2013)
is (SSC CHSL 2013)
The ratio of two numbers is 3 : 4 and their HCF is 5. Their LCM is: (SSC Sub. Ins. 2013)
If 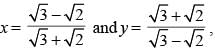 then the value of x3 + y3 is: (SSC Sub. Ins. 2013)
then the value of x3 + y3 is: (SSC Sub. Ins. 2013)
With a two digit prime number, if 18 is added, we get another prime number with digits reversed. How many such numbers are possible? (SSC CGL 2nd Sit. 2012)
If 13 + 23 + ....... + 93 = 2025, then the approx. value of (0.11)3 + (0.22)3 + ....... + (0.99)3 is (SSC CGL 2nd Sit. 2012)
The least number which when divided by 48, 64, 90, 120 will leave the remainders 38, 54, 80, 110 respectively, is (SSC CGL 2nd Sit. 2012)
What would be the sum of 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + ....... up to 15th term? (SSC CGL 2nd Sit. 2012)
The least multiple of 13 which when divided by 4, 5, 6, 7 leaves remainder 3 in each case is (SSC CGL 2nd Sit. 2012)
The next term of the series 1, 5 12, 24, 43 is (SSC CGL 1st Sit. 2012)
The next term of the series – 1, 6, 25, 62, 123, 214, _____ is: (SSC CGL 1st Sit. 2012)
The greatest number that will divide 19, 35 and 59 to leave the same remainder in each case is: (SSC CGL 1st Sit. 2012)