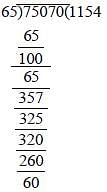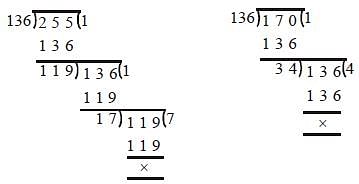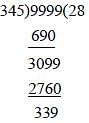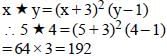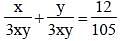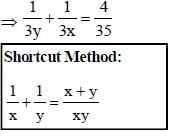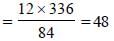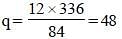SSC CGL Previous Year Questions: Number System and HCF & LCM- 3 - SSC CGL MCQ
30 Questions MCQ Test - SSC CGL Previous Year Questions: Number System and HCF & LCM- 3
A three-digit number 4a3 is added to an other three-digit number 984 to give the four digit number 13b7 which is divisible by 11. Then the value of (a + b) is: (SSC CGL 1st Sit. 2012)
The least number which when divided by 35, 45, 55 leaves the remainder 18, 28, 38 respectively is (SSC CGL 1st Sit. 2012)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number nearest to 75070 which is divisible by 65, is (SSC CGL 1st Sit. 2012)
There are 4 terms in an A.P. such that the sum of two means is 110 and product of their extremes is 2125. The 3rd term is (SSC Sub. Ins. 2012)
The greatest number that can divide 140, 176, 264 leaving remainders of 4, 6, and 9 respectively is (SSC Sub. Ins. 2012)
Four runners started running simultaneously from a point on a circular track. They took 200 seconds, 300 seconds, 360 seconds and 450 seconds to complete one round. After how much time they meet at the starting point for the first time? (SSC CGL 2nd Sit. 2011)
When 'n' is divisible by 5 the remainder is 2. What is the remainder when n^2 is divided by 5? (SSC CGL 2nd Sit. 2011)
L.C.M. of two numbers is 120 and their H.C.F. is 10. Which of the following can be the sum of those two numbers? (SSC CGL 2nd Sit. 2011)
Which one of the following will completely divide 571 + 572 + 573? (SSC CGL 2nd Sit. 2011)
If a * b = ab, then the value of 5 * 3 is (SSC CGL 2nd Sit. 2011)
The unit digit in the sum of (124)372 + (124)373 is (SSC CGL 2nd Sit. 2011)
If 17200 is divided by 18, the remainder is (SSC CGL 2nd Sit. 2011)
The least number, which is to be added to the greatest number of 4 digits so that the sum may be divisible by 345, is (SSC CGL 2nd Sit. 2011)
The traffic lights at three different road crossings change after 24 seconds, 36 seconds and 54 seconds respectively. If they all change simultaneously at 10 : 15 :00 AM, then at what time will they again change simultaneously? (SSC CGL 1st Sit. 2011)
A number when divided by 49 leaves 32 as remainder. This number when divided by 7 will have the remainder as (SSC CGL 1st Sit. 2011)
The L.C.M. of three different numbers is 120. Which of the following cannot be their H.C.F.? (SSC CGL 1st Sit. 2011)
If x * y = (x + 3)2 (y –1), then the value of 5 * 4 is (SSC CGL 1st Sit. 2011)
The last digit of (1001)2008 + 1002 is (SSC CGL 1st Sit. 2011)
The remainder when 321 is divided by 5 is (SSC CGL 1st Sit. 2011)
How many perfect squares lie between 120 and 300 ? (SSC CGL 2nd Sit. 2010)
If 'n' be any natural number, then by which largest number (n3 – n) is always divisible? (SSC CGL 2nd Sit. 2010)
The sum of two numbers is 36 and their H.C.F and L.C.M. are 3 and 105 respectively. The sum of the reciprocals of two numbers is (SSC CGL 2nd Sit. 2010)
The H.C.F. and L.C.M. of two numbers are 12 and 336 respectively. If one of the numbers is 84, the other is (SSC CGL 2nd Sit. 2010)
A 4–digit number is formed by repeating a 2–digit number such as 1515, 3737, etc. Any number of this form is exactly divisible by (SSC CGL 2nd Sit. 2010)
A number, when divided by 136, leaves remainder 36. If the same number is divided by 17, the remainder will be (SSC CGL 2nd Sit. 2010)
The sixth term of the sequence 2, 6, 11, 17, ..... is (SSC CGL 1st Sit. 2010)
Two numbers are in the ratio 3 : 4. Their L.C.M. is 84. The greater number is (SSC CGL 1st Sit. 2010)
A number, when divided by 114, leaves remainder 21. If the same number is divided by 19, then the remainder will be (SSC CGL 1st Sit. 2010)
The ninth term of the sequence 0, 3, 8, 15, 24, 35, .... is (SSC CGL 1st Sit. 2010)
The greatest number, which when subtracted from 5834, gives a number exactly divisible by each of 20, 28, 32 and 35, is (SSC CGL 1st Sit. 2010)