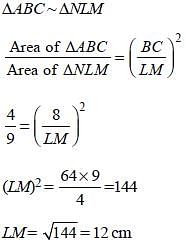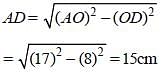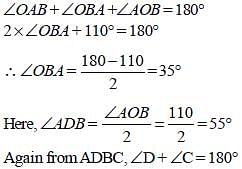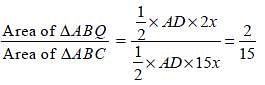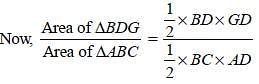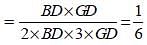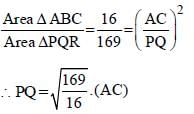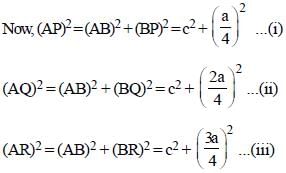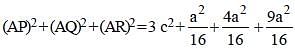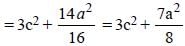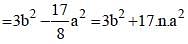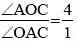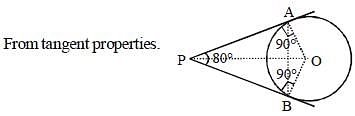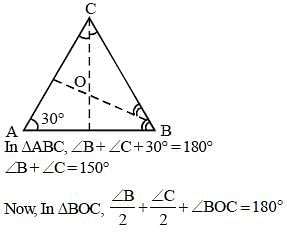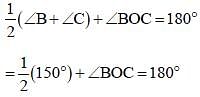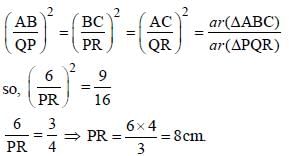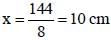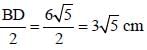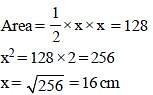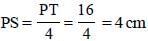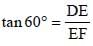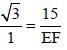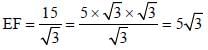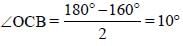All Courses
Get the App Signup / Login
Sign in Open App
SSC CGL Exam  >  SSC CGL Tests  >  SSC CGL Previous Year Questions: Geometry- 1 - SSC CGL MCQ

SSC CGL Previous Year Questions: Geometry- 1 - SSC CGL MCQ


Test Description

20 Questions MCQ Test - SSC CGL Previous Year Questions: Geometry- 1

SSC CGL Previous Year Questions: Geometry- 1 for SSC CGL 2024 is part of SSC CGL preparation. The SSC CGL Previous Year Questions: Geometry- 1 questions and answers have been prepared according to the SSC CGL exam syllabus.The SSC CGL Previous Year Questions: Geometry- 1 MCQs are made for SSC CGL 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for SSC CGL Previous Year Questions: Geometry- 1 below.
Solutions of SSC CGL Previous Year Questions: Geometry- 1 questions in English are available as part of our course for SSC CGL & SSC CGL Previous Year Questions: Geometry- 1 solutions in Hindi for SSC CGL course. Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free. Attempt SSC CGL Previous Year Questions: Geometry- 1 | 20 questions in 20 minutes | Mock test for SSC CGL preparation | Free important questions MCQ to study for SSC CGL Exam | Download free PDF with solutions
SSC CGL Previous Year Questions: Geometry- 1 - Question 1
Save

ΔABC ~ ΔNLM and ar(ΔABC) : ar(ΔLMN) = 4 : 9. If AB = 6 cm, BC = 8 cm and AC =12 cm, then ML is equal to:       (SSC CGL-2018)

Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 1

We have,

SSC CGL Previous Year Questions: Geometry- 1 - Question 2
Save

In a circle of radius 17 cm, a chord is at a distance of 8 cm from the centre of the circle. What is the length of the chord?       (SSC CGL-2018)

Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 2


Here, AB is a chord
OA = OB = 17cm (radius)
OD = 8cm
Form ΔADO

Chord AB = 2 ´ 15 = 30cm

1 Crore+ students have signed up on EduRev. Have you? Download the App
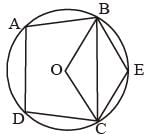
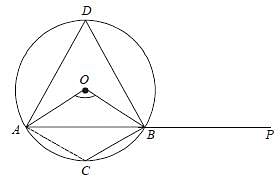
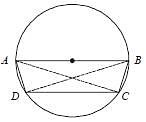
SSC CGL Previous Year Questions: Geometry- 1 - Question 3
Save

In a circle with centre O, an arc ABC subtends an angle of 110° at the centre of the circle. The chord AB is produced to a point P. Then ∠CBP is equal to:       (SSC CGL-2018)

Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 3


Here, OA = OB (radius of the circle).
∴ ∠OAB = ∠OBA
In ΔOAB,

∠C = 180° – 55° = 125°
∠CBP = 180° - 125° = 55°

SSC CGL Previous Year Questions: Geometry- 1 - Question 4
Save

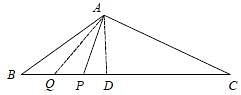
In ΔABC, P is a point on BC such that BP : PC = 4 : 11. If Q is the midpoint of BP, then ar(ΔABQ) : ar(ΔABC) is equal to:      (SSC CGL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 4


Here, BC = BP + PC
= 4x + 11x = 15x
and BQ = PQ = 2x
Let AD is the height of the ΔABC,

SSC CGL Previous Year Questions: Geometry- 1 - Question 5
Save

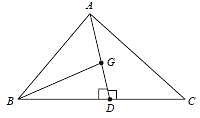
In ΔABC, AD is the median and G is a point on AD such that AG : GD = 2 : 1. Then ar(ΔBDG) : ar(ΔABC) is equal to:       (SSC CGL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 5


Let ΔABC is a equilateral triangle in which AD is a median.
Then, ∠ADB = 90° {∵ ΔABC is equilateral)

SSC CGL Previous Year Questions: Geometry- 1 - Question 6
Save

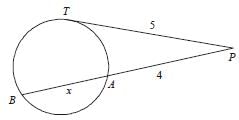
From a point P outside a cir cle, PAB is a secan t and PT is a tangent to the circle, where, A, B and T are points on the circle. If PT = 5 cm, PA = 4 cm and AB = x cm, then x is equal to:       (SSC CGL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 6


From circle properties
PT2 = PA ´ PB
(5)2 = 4 x (x + 4)
x + 4 = (25/4) = 6.25
x = 6.25 – 4 = 2.25 cm

SSC CGL Previous Year Questions: Geometry- 1 - Question 7
Save

ΔABC ~ ΔRQP and AB = 4 cm, BC = 6 cm and AC = 5 cm. If ar(ΔABC) : ar(ΔPQR) = 9 : 4, then PQ is equal to:       (SSC CGL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 7

SSC CGL Previous Year Questions: Geometry- 1 - Question 8
Save

In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC = 40°, then ∠CAD is equal to:       (SSC CGL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 8


As AB is a diameter.
∠ACB = ∠ADB = 90°
In Δ ABC, ∠BCA = 90°
∠BAC = 40°
∴ ∠ABC = 180° – 90° – 40° = 50°
and ABCD is cyclic trapezium
so, ∠ABC + ∠ADC = 180°
∴ ∠ADC = 180° – ∠ABC
= 180° – 50° = 130°
and ∠DCA = ∠BAC = 40° {∵ AB || CD}.
Now, In ΔACD, ∠CAD = 180°– (∠ADC + ∠ACD)
= 180° – (130° + 40°) = 10°

SSC CGL Previous Year Questions: Geometry- 1 - Question 9
Save

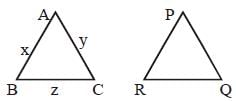
It is given that ΔABC ~ ΔPRQ and that Area ABC : Area PRQ = 16 : 169. If AB = x, AC = y,  BC = z (all in cm), then PQ is equal to:      (SSC CHSL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 9



= 13/4 y.

SSC CGL Previous Year Questions: Geometry- 1 - Question 10
Save

The side BC of a right-angled triangle ABC (∠ABC = 90º) is divided into four equal parts at P, Q and R respectively. If AP2 + AQ2 + AR2 = 3b2 + 17na2, then n is equal to :       (SSC CHSL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 10


In ΔABC, AB = c, BC = a, and AC= b.
and BP = PQ = QR = RC = a/4.

from (i) + (ii) + (iii)


Again from ΔABC, b2 = c2 + a2
c2 = b2 – a2
∴ AP2 + AQ2 + AR2 = 3 (b2 – a2) + 7a2/8


Hence, n = - (1/8).

SSC CGL Previous Year Questions: Geometry- 1 - Question 11
Save

A and B are two points on a circle with centre O. AT is a tangent, such that ∠BAT = 45º. N is a point on OA, such that BN = 10 cm. The length of the median OM of the Δ NOB is :       (SSC CHSL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 11


As AT is a tangent ∴∠ OAT = 90°
Again ∠ BAT = 45°
∴ ∠ OAB = 90° – 45° = 45°
In Δ AOB, OA = OB,
∴ ∠ OAB = ∠ OBA = 45° then ∠ NOB= 180° – 45° – 45° = 90° and Δ BON is also a right angle triangle.
Now, OM is a median of ΔBON,
∴ OM divide BN in two equal part
∴ BM = OM = 5 cm

SSC CGL Previous Year Questions: Geometry- 1 - Question 12
Save

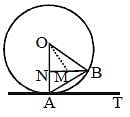
OABC is a quadrilateral, where O is the centre of a circle and A, B, C are points in the circle, such that ∠ABC = 120º. What is the ratio of the measure of ∠AOC to that of ∠OAC?       (SSC CHSL-2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 12

Ratio of 

SSC CGL Previous Year Questions: Geometry- 1 - Question 13
Save

PA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB = 80°, then ∠OAB is equal to:       (SSC Sub. Ins. 2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 13


∠PAO = 90°
and ∠OPA = 80°/2 = 40°
In Δ AOP, ∠AOP + ∠APO + ∠PAO = 180°
∠AOP + 40° + 90° = 180°
∴∠AOP = 180° – 130° = 50°

SSC CGL Previous Year Questions: Geometry- 1 - Question 14
Save

ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC = 145°. What is the measure of ∠BAC?        (SSC Sub. Ins. 2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 14


As ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
∠B + 145° = 180°
∠B = 180° – 145° = 35°
Again as AB is a diameter.
∴ ∠ACB = 90°
Now, In ΔACB, ∠ BAC + ∠ABC + ∠ACB = 180°
∠BAC + 35° + 90° = 180°
∠BAC = 180° – 90° – 35° = 55°.

SSC CGL Previous Year Questions: Geometry- 1 - Question 15
Save

In ΔABC, ∠A = 30°. If the bisectors of the angle B and angle C meet at a point O in the interior of the triangle, then ∠BOC is equal to:      (SSC Sub. Ins. 2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 15



= 75° + ∠BOC = 180°
∠BOC = 180° – 75° = 105°

SSC CGL Previous Year Questions: Geometry- 1 - Question 16
Save

Let ΔABC ~ ΔQPR and 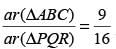. If AB = 12cm, BC = 6cm and AC = 9cm. Then PR is equal to:      (SSC Sub. Ins. 2018)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 16


As ΔABC ~ ΔQPR, then

SSC CGL Previous Year Questions: Geometry- 1 - Question 17
Save

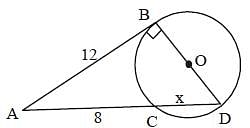
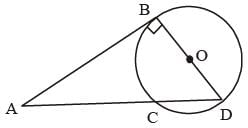
In the given figure , BD passes through centr e O, AB = 12 and AC = 8. What is the radius of the circle?       (SSC Sub. Ins. 2017)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 17


According to question,
AB = 12
AC = 8
AD = 8 + x
As, we know that
(AB)2 = AC × AD
(12)2 = 8 × (8 + x)
∴
ΔABD is a right angle because ∠B = 90°
By Pythagorean theorem,
BD2 + AB2 = AD2
BD2 + AB2 = AD2
BD2 = (18)2 – (12)2 {Here AD = 8 + 10 = 18 cm}
= 324 – 144 = 180
∴ BD = 6√5 cm
∴ Radius = 

SSC CGL Previous Year Questions: Geometry- 1 - Question 18
Save

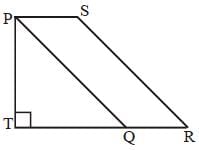
In the given figure, area of isosceles triangle PQT is 128 cm2 and QT = PQ and PQ = 4 PS, PT || SR, then what is the area (in cm2) of the quadrilateral PTRS?        (SSC Sub. Ins. 2017)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 18


From question, PT = TQ = x (Let)

Again, 
As PQ || RS and PS || QR (By symmetry)
∴ PQRS is a parallelogram with base (b) = 4 cm height (h) = PT = 16 cm
Area = b × h = 4 × 16 = 64 cm2

SSC CGL Previous Year Questions: Geometry- 1 - Question 19
Save

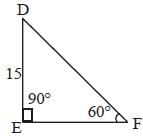
If ΔDEF is right angled at E, DE = 15 and ∠DFE = 60°, then what is the value of EF?       (SSC Sub. Ins. 2017)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 19

According to question,
DE = 15, EF = ?
∠DFE = 60°
∠DEF = 90°

∴ 

∴ 

SSC CGL Previous Year Questions: Geometry- 1 - Question 20
Save

In the given figure, O is the centre of the circle, ∠DAB = 110°and ∠BEC = 100°. What is the value (in degrees) of ∠OCB?            (SSC Sub. Ins. 2017)
Detailed Solution for SSC CGL Previous Year Questions: Geometry- 1 - Question 20


∠BEC = 100° (given)
Quadrilateral BECF are cyclic
So, ∠BEC + ∠BFC = 180°
100° + ∠BFC = 180°
⇒ ∠BFC = 180° – 100° = 80°
Now, ∠BOC = 2 × ∠BFC (Angle made by the same chord at the center)
= 2 × 80° = 160°
In ΔOBC, OB = OC (radius)
∴ ∠OBC = ∠OCB
Now, ∠BOC + ∠OBC + ∠OCB = 180°
160° + 2∠OCB = 180°
⇒ 

Information about SSC CGL Previous Year Questions: Geometry- 1 Page
In this test you can find the Exam questions for SSC CGL Previous Year Questions: Geometry- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for SSC CGL Previous Year Questions: Geometry- 1, EduRev gives you an ample number of Online tests for practice

Top Courses for SSC CGL

Download as PDF

Top Courses for SSC CGL

Important Questions for SSC CGL Previous Year Questions: Geometry- 1

Find all the important questions for SSC CGL Previous Year Questions: Geometry- 1 at EduRev.Get fully prepared for SSC CGL Previous Year Questions: Geometry- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the SSC CGL Previous Year Questions: Geometry- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of SSC CGL Previous Year Questions: Geometry- 1 resources.

SSC CGL Previous Year Questions: Geometry- 1 MCQs with Answers

Prepare for the SSC CGL Previous Year Questions: Geometry- 1 within the SSC CGL exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for SSC CGL Previous Year Questions: Geometry- 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace SSC CGL Previous Year Questions: Geometry- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup