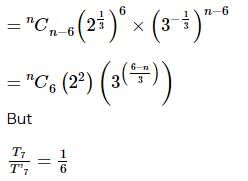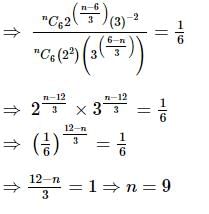BITSAT Mathematics Test - 8 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 8
If the mth term of an AP is n and the nth term is m, then write its pth term
An unbiased die is rolled until a number greater than 4 appears. The probability that an even number of trials are needed, is:
The solution to the differential equation dy/dx = e3x - 2y + x2e-2y is:
In a ΔABC, if a = 18 , b = 24 and c = 30 then find the value of sin (A/2) ?
If  are vectors such that
are vectors such that 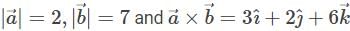 then what is the acute angle between
then what is the acute angle between 
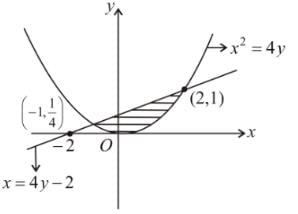
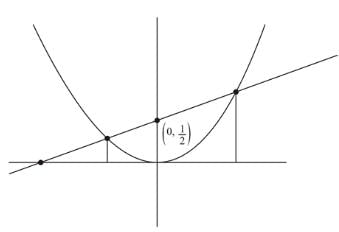
The area bounded by the curve x2 = 4y and the straight line x = 4y − 2 is
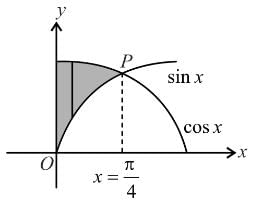
The area bounded by the curves y = sin x, y = cosx and y-axis in first quadrant is
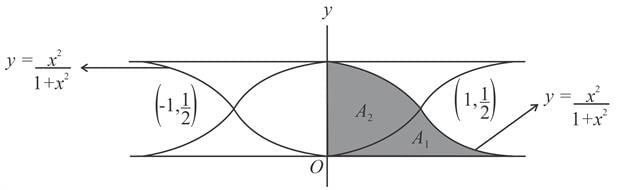
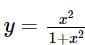 divides the area enclosed by
divides the area enclosed by 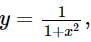 x-axis and y-axis in the first quadrant in the ratio
x-axis and y-axis in the first quadrant in the ratio
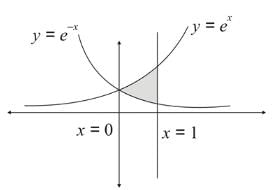
The area (in sq. units) of the region bounded by y = ex, y = e−x, x = 0 and x = 1 is
Area enclosed by the curve y = f(x) defined parametrically as 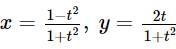 is
is
If the area bounded by y = ax2 and x = ay2, a > 0, is 1 sq. unit, then a =
Assertion: The area of the region {(x, y) : x2 + y2 ≤ 5, ||x| − |y|| ≥ 1} is 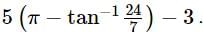
Reason: 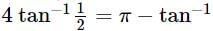
The area of the region bounded by the x− axis and the curves defined by y = tan x, 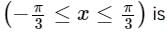
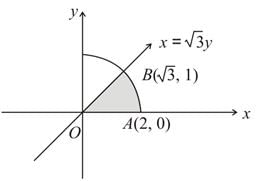
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4, the line x = y√3 and x−axis is
The number of irrational terms in the expansion of 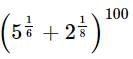 is
is
The coefficient of x1012 in the expansion of (1 + xn + x253)10, (where n ≤ 22 is any positive integer), is
If the second term in the expansion 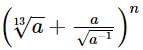 (n ∈ N) is 14a5/2, then n is equal to
(n ∈ N) is 14a5/2, then n is equal to
The least positive integral value of x which satisfies the inequality 10Cx−1 > 210Cx is
If the second term of the expansion 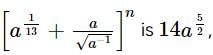 then the value of
then the value of 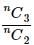 is
is
If last three digits of the expression 17256 are A1,A2 & A3 respectively, then the value of expression 2A2 + A3 − 4A1 equals
If (5 + 2√6)n = I + f ; n, I ∈ N and 0 ≤ f < 1, then I equals
If in the expansion of 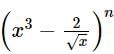 a term like x2 exists and n is a double-digit number, then least value of n is
a term like x2 exists and n is a double-digit number, then least value of n is
If the ratio of the 7th term from the beginning to the 7th term from the end in the expansion of 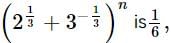 then the value of n is
then the value of n is


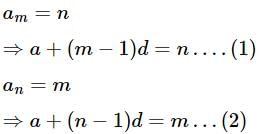
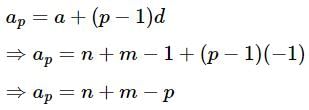
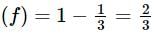

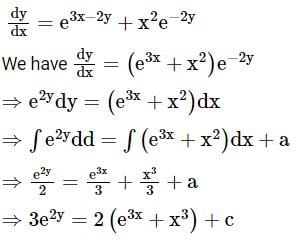

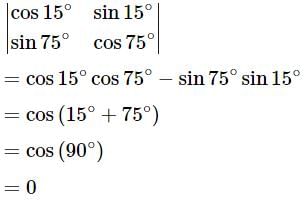
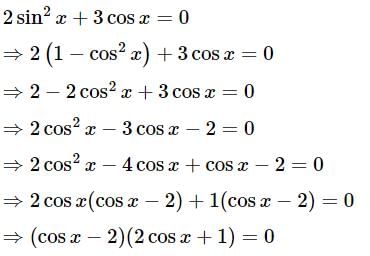
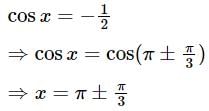

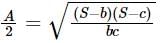
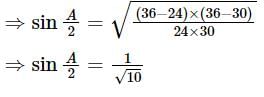
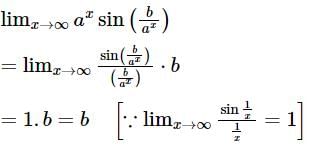
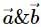 is given by
is given by 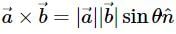
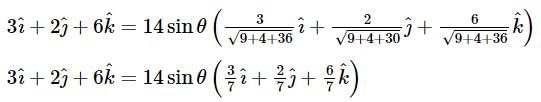
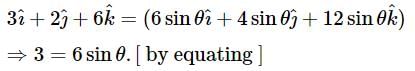
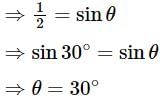
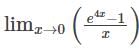 is equal to?
is equal to?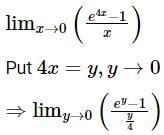

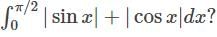
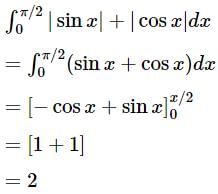
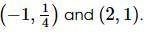
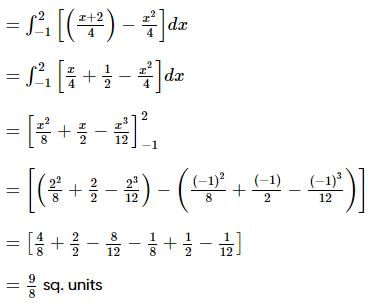
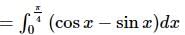
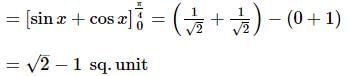
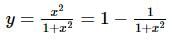
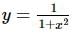
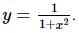
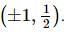
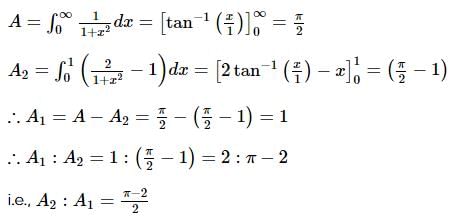
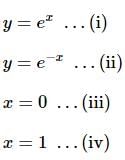
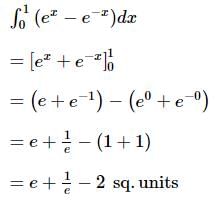
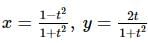
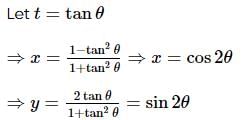
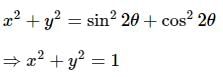
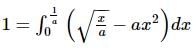
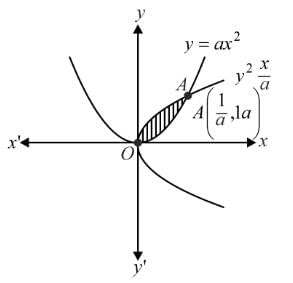
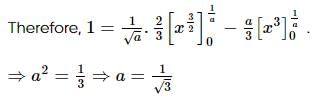
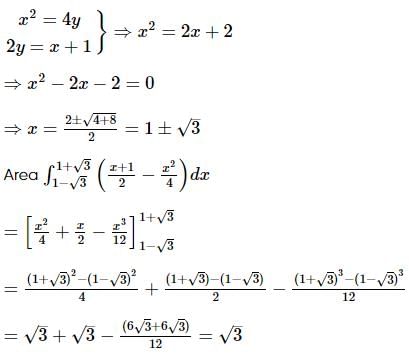
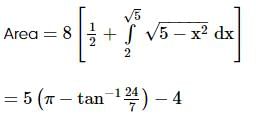
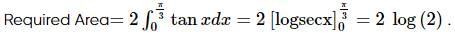
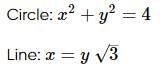
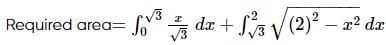
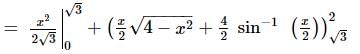
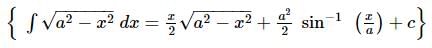

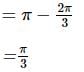
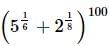 is given by
is given by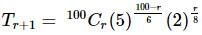
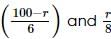 are both integers i.e., if (100−r) is a multiple of 6 and r is a multiple of 8.
are both integers i.e., if (100−r) is a multiple of 6 and r is a multiple of 8.
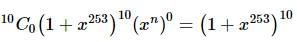

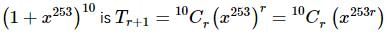
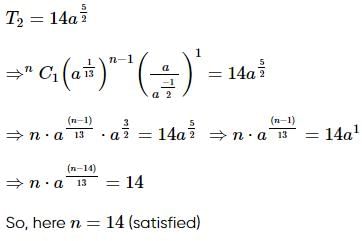
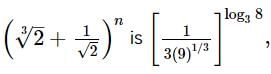 then the fifth term is
then the fifth term is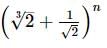
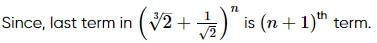

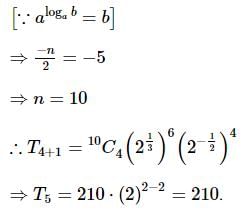
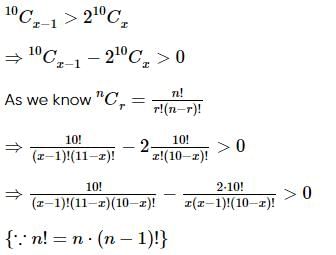
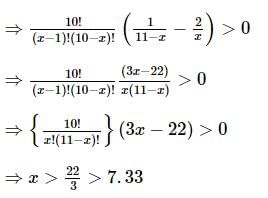
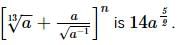
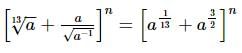
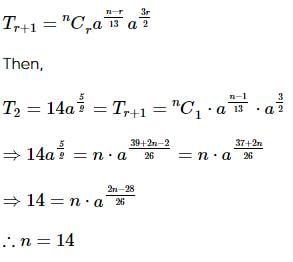
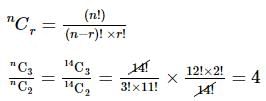
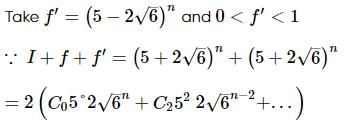
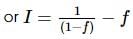
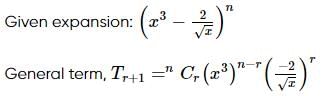
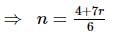
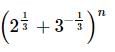
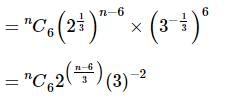
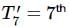 term from the end
term from the end