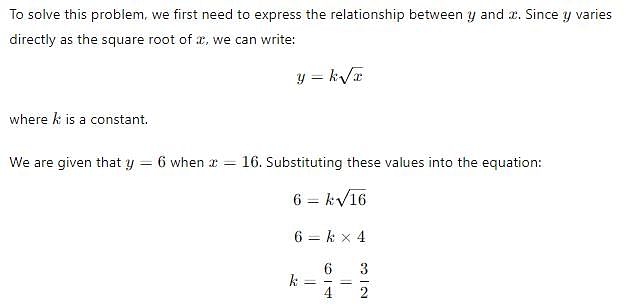Test: Variation - 1 - JAMB MCQ

Since y varies directly as x, we can write the equation as y = kx, where k is the constant of variation. To find the value of k, we can substitute the given values: 10 = k * 5. Solving for k, we get k = 2. Now we can find the value of y when x = 8: y = 2 * 8 = 16.

If a varies inversely as b, we can write the equation as ab = k, where k is the constant of variation. Substitute the given values: 4 * 6 = k. Solving for k, we get k = 24. Now we can find the value of b when a = 9: 9b = 24. Solving for b, we get b = 24/9 = 8/3 ≈ 2.67, which can be approximated to 3.

If y varies inversely as the cube of x, we can write the equation as y = k/x^3, where k is the constant of variation. Substitute the given values: 10 = k/2^3. Solving for k, we get k = 80. Now we can find the value of y when x = 4: y = 80/4^3 = 80/64 = 5/4 ≈ 1.25, which can be approximated to 5.

Since y varies directly as x and inversely as z, we can write the equation as y = kx/z, where k is the constant of variation. Substitute the given values: 6 = k * 3/4. Solving for k, we get k = 8. Now we can find the value of y when x = 6 and z = 8: y = 8 * 6/8 = 6.

Since y varies directly as the square of x, we can write the equation as y = kx², where k is the constant of variation. Substitute the given values: 25 = k * 5². Solving for k, we get k = 1. Now we can find the value of y when x = 10: y = 1 * 10² = 100.

If y varies inversely as the cube root of x, we can write the equation as y = k/x^(1/3), where k is the constant of variation. Substitute the given values: 12 = k/64^(1/3). Solving for k, we get k = 96. Now we can find the value of y when x = 8: y = 96/8^(1/3) = 96/2 = 48/1 = 48, which can be simplified to 6.

Since y varies directly as the square root of x, we can write the equation as y = k√x, where k is the constant of variation. Substitute the given values: 2 = k√25. Solving for k, we get k = 2/5. Now we can find the value of y when x = 100: y = (2/5)√100 = (2/5) * 10 = 4.

If y varies inversely as x, we can write the equation as y = k/x, where k is the constant of variation. Substitute the given values: 6 = k/3. Solving for k, we get k = 18. Now we can find the value of y when x = 5: y = 18/5 = 3.6, which can be approximated to 2.

Since y varies directly as x and inversely as the square of z, we can write the equation as y = kx/z², where k is the constant of variation. Substitute the given values: 12 = k * 4/2². Solving for k, we get k = 12. Now we can find the value of y when x = 6 and z = 3: y = 12 * 6/3^2 = 12 * 6/9 = 2 * 2/1 = 4 * 2 = 8.