Test: Geometry - GMAT MCQ
10 Questions MCQ Test - Test: Geometry
On the segment PS above, PS = 10. What is the length of the middle segment QR?
(1) PR = 7
(2) QS = 6
(2) QS = 6
In isosceles triangle RST what is the measure of angle R?
(1) The measure of ∠T is 100°.
(2) The measure of ∠S is 40°.
(2) The measure of ∠S is 40°.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the number of 360-degree rotations that a unicycle wheel made while rolling 150 feet in a straight line without slipping?
(1) The diameter of the unicycle wheel, including the 2 inch tire, was 18 inches.
(2) The wheel traveled 3 inches after it rotated 60°.
(2) The wheel traveled 3 inches after it rotated 60°.
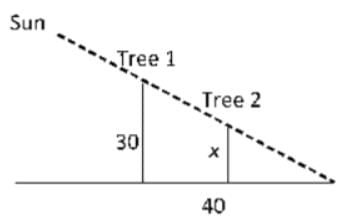
As the figure shown above, the taller tree is 30 feet high and has a 40 feet shadow. What is the height of the shorter tree?
(1) The shorter tree has a 22 feet shadow.
(2) The distance between two trees is 18 feet.
Is quadrilateral MNOP a square?
(1) MN = NO = OP
(2) Angle N and angle O are right angles
What is the volume of a certain cube?
(1) The cube has a width of 5 cm
(2) The cube has a surface area of 150 cm
How many books will fit into a drawer?
(1) Each book has a volume of 10 cubic centimeters.
(2) The drawer is 300 centimeters by 30 centimeters by 20 centimeters and has the shape of a rectangular solid.
What is the volume of cube C?
(1) The length of the space diagonal of cube C is √3 inches.
(2) The length of the diagonal of the base of cube C is √2 inches.
What is the area of right triangle ABC?
(1) Side AB measures 5 meters and Side BC measures 13 meters
(2) Angle ABC measures 90 degrees.
Is quadrilateral a square?
(1) Three angles of a quadrilateral are 90 degrees each.
(2) 3 sides of a quadrilateral are equal in length.


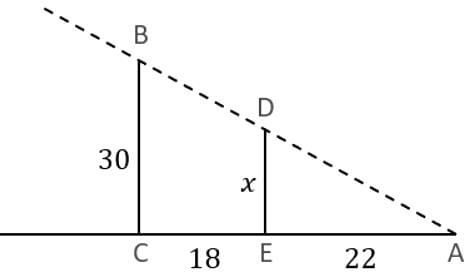
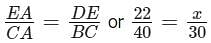 to get the value of x
to get the value of x














