Test: Number Properties - GMAT MCQ
10 Questions MCQ Test - Test: Number Properties
A bag is filled with blue, green, purple and red chips worth 2, 5, x and 13 points each, respectively. The worth of a purple chip is more than the worth of a green chip, but less than that of a red chip. A certain number of chips are selected randomly from the bag. If the product of the points of the selected chips is 13,689,000, how many purple chips were selected?
The product (8)(888...8), where the second factor has k digits, is an integer whose digits have a sum of 1000. What is k?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For any integer P greater than 1, P! denotes the product of all the integers from 1 to P, inclusive. If 10! Is divisible by 10080*h and h is a perfect square, what is the greatest possible value of h?
In a company with 48 employees, some part-time and some full-time, exactly (1/3) of the part-time employees and (1/4) of the full-time employees take the subway to work. What is the greatest possible number of employees who take the subway to work?
How many even number in the range between 10 to 100 inclusive are not divisible by 3
If N is a positive integer and 14N/60 is an integer, then N has how many different positive prime factors?
If the sum of the consecutive integers from –42 to n inclusive is 372, what is the value of n?
P and Q are two two-digit numbersTheir product equals the product of the numbers obtained on reversing them. None of the digits in P or Q is equal to the other digit in it or any digit in the other number. The product of tens digits of the two numbers' is a composite single digit number. How many ordered pairs (P, Q) satisfy these conditions?



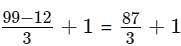 = 30 of which half will be even numbers. = 15.
= 30 of which half will be even numbers. = 15.














