Practice Test for NMAT - 8 - CAT MCQ
30 Questions MCQ Test - Practice Test for NMAT - 8
Ramesh can till his plot of land in 10 hours. Suresh can till a plot that is double the size of Ramesh’s plot in 40 hours. Both of them decide to till another plot equal in size to Ramesh’s plot together. They work alternately for 1 hour starting with Suresh. How much time do they take to till the plot?
Group Question
Answer the following question based on the information given below.
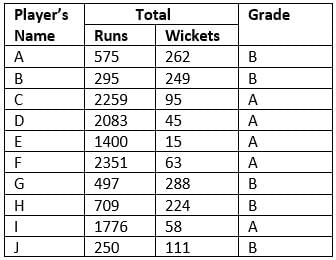
The following table shows the total runs scored and wickets taken by 10 Indian players in 10 different matches against each five different countries.

According to their performance, players are allotted a grade group. The five batsmen scoring the maximum runs are given grade A. The five bowlers taking the maximum wickets are given grade B. The performance of any player having grade A is said to be better than that of any other player having grade A, if the former scored more runs than the latter against at least three countries. The performance of any player having grade B is said to be better than that of any other player having grade B, if the former took more wickets than the latter against at least three countries.
NOTE: Round-off any decimal number to the nearest integer.
Q. Who was the minimum run scorer among the players who got grade A and who took minimum wickets among the players who got grade B?
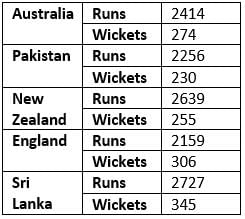
The following table shows the total runs scored and wickets taken by 10 Indian players in 10 different matches against each five different countries.
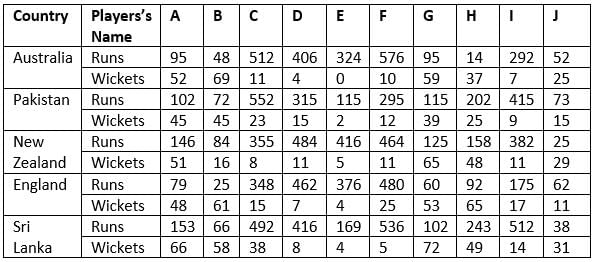
According to their performance, players are allotted a grade group. The five batsmen scoring the maximum runs are given grade A. The five bowlers taking the maximum wickets are given grade B. The performance of any player having grade A is said to be better than that of any other player having grade A, if the former scored more runs than the latter against at least three countries. The performance of any player having grade B is said to be better than that of any other player having grade B, if the former took more wickets than the latter against at least three countries.
NOTE: Round-off any decimal number to the nearest integer.
Q. How many players performed better than E?
The following table shows the total runs scored and wickets taken by 10 Indian players in 10 different matches against each five different countries.
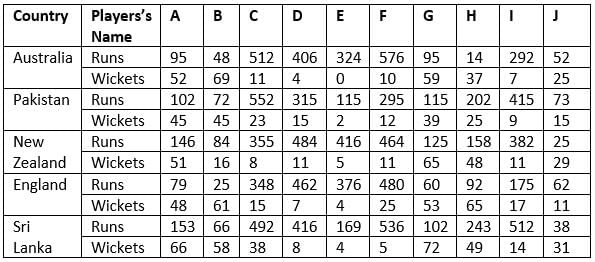
According to their performance, players are allotted a grade group. The five batsmen scoring the maximum runs are given grade A. The five bowlers taking the maximum wickets are given grade B. The performance of any player having grade A is said to be better than that of any other player having grade A, if the former scored more runs than the latter against at least three countries. The performance of any player having grade B is said to be better than that of any other player having grade B, if the former took more wickets than the latter against at least three countries.
NOTE: Round-off any decimal number to the nearest integer.
Q. Against which country did Indian players perform the best?
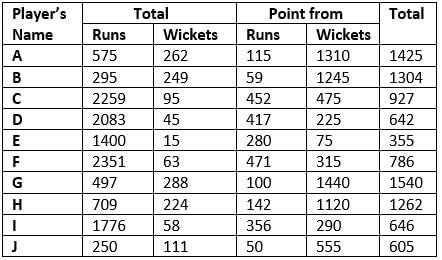
The following table shows the total runs scored and wickets taken by 10 Indian players in 10 different matches against each five different countries.
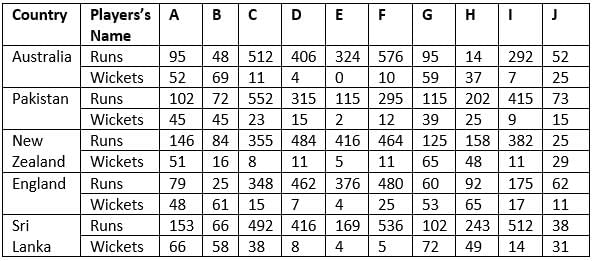
According to their performance, players are allotted a grade group. The five batsmen scoring the maximum runs are given grade A. The five bowlers taking the maximum wickets are given grade B. The performance of any player having grade A is said to be better than that of any other player having grade A, if the former scored more runs than the latter against at least three countries. The performance of any player having grade B is said to be better than that of any other player having grade B, if the former took more wickets than the latter against at least three countries.
NOTE: Round-off any decimal number to the nearest integer.
Q. If any player scored runs between 1 to 5, he gets 1 point, if he scored between 6 to 10 runs, he gets 2 points and so on. For each wicket, the player gets 5 points. How many players have more than 784 points?
What will be the value of a + b + c + d, if 6893a98b is divisible by 11 and 8 and 592200c9d is divisible by 8 and 9?
Amir buys a kilo of sweets at Rs. x. He then marks it up 20%. What should be the discount given by Amir so that he gains 10% on his transaction?
The sum of the first fifteen terms of an arithmetic progression is 40 more than the sum of the first seven terms of the same arithmetic progression. What is the sum of the first twenty two terms of the same progression?
Anil and Jacky open a firm. Initially Jacky makes 60% of the total investment and Anil makes 40% of the total investment. After 8 months, Jacky removes 30% of what he had invested and Anil increases his investment in such a way that the total initial investment remains constant. After certain number of months they receive Rs. 18,000 as profit and they divide it equally. If they divide the profit based on their investment then what is the average monthly profit of each during the specified period?
Group Question
Answer the following question based on the information given below.
The bar-graph below shows the profit percentage earned by Abhinaya’s company for six consecutive years starting from 2002.
Profit percentage(P%) = Profit(P) / Expenditure(E) x 100
Income(I) = Profit(P) + Expenditure(E)
Q. If the incomes in 2003 and 2004 were the same, what is the ratio of profit in 2003 to that of profit in 2004?
The bar-graph below shows the profit percentage earned by Abhinaya’s company for six consecutive years starting from 2002.
Profit percentage(P%) = Profit(P) / Expenditure(E) x 100
Income(I) = Profit(P) + Expenditure(E)
Q. If the expenditure in 2005 was half the income in 2002, what was the ratio of the income in 2002 to the income in 2005?
The bar-graph below shows the profit percentage earned by Abhinaya’s company for six consecutive years starting from 2002.
Profit percentage(P%) = Profit(P) / Expenditure(E) x 100
Income(I) = Profit(P) + Expenditure(E)
Q. If the expenditure is 2007 was Rs. 4 lakhs and the ratio of the profit in 2007 to the profit in 2006 was 2:3, what was the expenditure (in Rs.) in 2006?
The bar-graph below shows the profit percentage earned by Abhinaya’s company for six consecutive years starting from 2002.
Profit percentage(P%) = Profit(P) / Expenditure(E) x 100
Income(I) = Profit(P) + Expenditure(E)
Q. Return on Investment is calculated as the ratio of Income to Expenditure. Thus, income : expenditure = 2 : 1 implies a 100% return on investment. If the expenditure in each year was the same, what was the overall ROI for the entire period?
An examination has 120 questions with 40 questions each in three sections. In section I, a student gets 3 marks for a correct answer and (-1.5) marks for a wrong answer. In section II, a student gets 2 marks for a correct answer and (-1) mark for a wrong answer. In section III, a student gets 1 mark for a correct answer and (-0.5) marks for a wrong answer. Suvidh attempted all the questions and got a total of 60 marks in the examination. If Suvidh had attempted 30 questions of section III correctly, then what was the maximum number of questions that Suvidh could have answered incorrectly on the whole?
A ship travels from port Sakini to port Dakini in 20 hours against the stream. On another day it starts from port Sakini and takes 7 hours to go to port Sankini and come back. Both the ships travel with same speed. Port Sankini lies on the way from port Sakini to port Dakini at a distance equal to one fourth of the distance between port Sakini to port Dakini. Find the time taken by the ship to go from port Dakini to port Sankini and come back.
There are three groups of students in a college - Group A, Group B and Group C. The average of points scored on sports day by students of Group A, Group B and Group C are 70, 60 and 75 respectively. The average of points scored by students of Group B and Group C together is 65 and the average of points scored by students of Group A and Group C together is 72. What is the average of points scored by students of the three groups together?
Group Question
Answer the following questions based on the information given below.
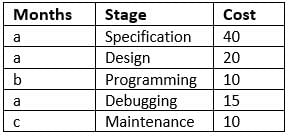
A software company offers client the entire product suite - starting from specifications to maintenance of the delivered product. Its time frame for each stage along with cost (in Rs. ’000' per man-month) charged to client is as shown below. The stages follow each other in the given sequence and no two stages overlap.
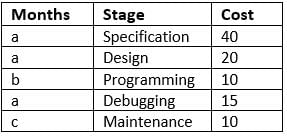
Over the duration of the entire project, it allocates people to the project as per the table given below:

Q. On a certain project, the company earns Rs. 6,85,000. If the Design stage lasts two months, for how many months does the company provide maintenance?
A software company offers client the entire product suite - starting from specifications to maintenance of the delivered product. Its time frame for each stage along with cost (in Rs. ’000' per man-month) charged to client is as shown below. The stages follow each other in the given sequence and no two stages overlap.
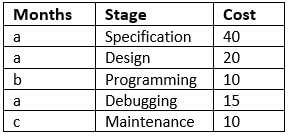
Over the duration of the entire project, it allocates people to the project as per the table given below:

Q. With reference to the above question, what is the cost charged by the company for the Programming stage?
A software company offers client the entire product suite - starting from specifications to maintenance of the delivered product. Its time frame for each stage along with cost (in Rs. ’000' per man-month) charged to client is as shown below. The stages follow each other in the given sequence and no two stages overlap.
Over the duration of the entire project, it allocates people to the project as per the table given below:

Q. If the Programming and Maintenance stages takes two-thirds the total time required for the remaining stages, what amount does the company spend on programming?
A software company offers client the entire product suite - starting from specifications to maintenance of the delivered product. Its time frame for each stage along with cost (in Rs. ’000' per man-month) charged to client is as shown below. The stages follow each other in the given sequence and no two stages overlap.
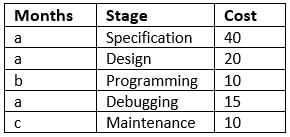
Over the duration of the entire project, it allocates people to the project as per the table given below:

Q. With reference to the previous question, what stage would the company be working on in February if it starts the project on 1st March and Programming takes twice the time that Maintenance takes?
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
EFH is an isosceles triangle with EF = EH. If EG is the bisector of FH, what is the length of FG (in cm)?
A. EF = 10 cm
B. EG = 7 cm
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Q. What is the first term of the geometric progression?
A. The sum of the first three terms of the progression is 13.
B. The product of the first three terms of the progression is 27.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Pipes A and B can together fill a tank in 24 hours. If the filling capacity of pipe A is doubled and that of pipe B is tripled, then both the pipes together will take x hours to fill the tank. What is the value of x?
A. x is a prime number.
B. x is an integer greater than 10.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Is p > q, if both p and q are integers?
A. p2 > q2
B. |p| > |q|
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
Radha reads a book from start to end (without breaks) at a uniform speed. When does Radha finish reading the book?
A. Radha starts reading at 9:00 a.m.
B. On the same day, Radha finishes reading a quarter of the book at 11:45 a.m. and three-quarters of the book by 5:15 p.m.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
A family has only one kid. The father says “After n years, my age will be 4 times the age of my kid”. The mother says “after n years, my age will be 3 times that of my kid”. What would be the combined age of parents after n years?
A. The age difference between the parents is 10 years.
B. After 'n' years the kid is going to be twice as old as she is now.
How many five digit odd numbers having distinct digits can be formed using the digits 1, 2, 6, 7, 8 and 9 such that there are exactly two odd digits in the number?