Test: Permutation And Combination- 2 - GMAT MCQ
20 Questions MCQ Test - Test: Permutation And Combination- 2
A triangle is to be constructed in the xy-plane such that the x- and y- coordinates of each vertex are integers that satisfy the inequalities -3 ≤ x < 7 and 2 < y ≤ 7. If one of the sides is parallel to the x-axis, how many different triangles with these specifications can be constructed?
The players for a Tennis Mixed Doubles match are to be chosen from among 5 men and 4 women. In how many ways can the teams for the match be formed?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A soccer team of 11 players is to be formed out of a pool of 23 available players. The team should consist of 3 strikers, 4 midfielders, 3 defenders and 1 goalkeeper. The pool of 23 players consists of 6 strikers, 7 midfielders, 7 defenders and 3 goalkeepers. If Bruce, who is a striker, and David, who is a midfielder, should be a part of the team, what is the number of possible ways in which the team can be formed?
How many 3-letter words can be formed using the letters from the word GALE, if repetition is not allowed?
How many 4 digit numbers greater than 4000 can be formed using the digits from 0 to 8 such that the number is divisible by 4?
A company interviewed 5 applicants each for the posts of the Director and the President. If Jack and Jill were the only applicants who were interviewed for both the posts and an applicant can be selected for only one of the posts, what is the number of ways in which the company can select its Director and President from the interviewed applicants?
How many positive 4-digit integers are divisible by 20 if the repetition of digits is not allowed?
A salesman has five chocolates each of three different varieties. If he has to sell 9 chocolates to 9 different people and he can sell at most two varieties of chocolates, in how many different ways can he sell the chocolates?
The figure above shows the different alternate routes possible to go from point A to point E. The arrows show the allowed direction of motion on each route. What is the total number of ways to go from point A to E?
The editor of an anthology of short stories has to select authors from a pool of 12 authors, of which 4 are female. If the anthology is to include the work of 8 authors of which at least 2 must be female, in how many ways can the editor select the authors?
The figure above shows a rectangle ABCD in the xy- coordinate plane. The sides AB and AD are parallel to the x- and the y- axis respectively. How many squares of side 1 unit that lie on or inside the rectangle ABCD can be drawn?
(1) The length of side AB is 6 units
(2) The coordinates of points A and C are (3,2) and (9, 5)
The lowest integer that has both positive integers x and y as its factors can be written in the form of If x can be written as
, where a, b, c and d are positive integers, what are the possible number of values that y can take ?
A code is formed by combining one of the letters from A- Z and two distinct digits from 0 to 9 such that if the letter in the code is a vowel, the sum of the digits in the code should be even and if the letter in the code is a consonant, the sum of the digits in the code should be odd. If the code is case-sensitive (for example, A is considered to be different from a), how many different codes are possible?
Micky has 10 different letters and 5 different envelopes with him. If he can only put one letter in an envelope, in how many ways can the letters be put in the envelopes?
In how many ways can 12 different books be distributed equally among 4 different boxes?
The host of a television debate show has to select a 4-member discussion panel out of a list of 22 willing candidates that includes 5 politicians and 6 businessmen. If the list includes candidates from at least 4 professions and no two members of the discussion panel are to be of the same profession, then in how many ways can the panel be constituted?
(1) The list includes 5 journalists and 2 authors
(2) The list includes only 1 profession from which there are fewer than 3 candidatesStatement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
What is the value of even positive integer n?
(1) The number of ways to choose 2 items out of n distinct items is 28
(2) The number of ways to choose 2 prime numbers out of the first n/2 positive integers is 1
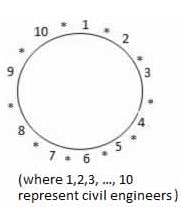
In how many ways can 10 software engineers and 10 civil engineers be seated in a round table so that they are positioned alternatively?
How many numbers not exceeding 10000 can be made using the digits 2,4,5,6,8 if repetition of digits is allowed?
In how many ways can 7 identical balls be distributed in 5 different boxes if any box can contain any number of balls?