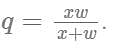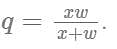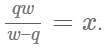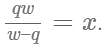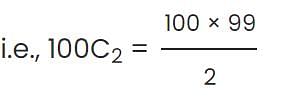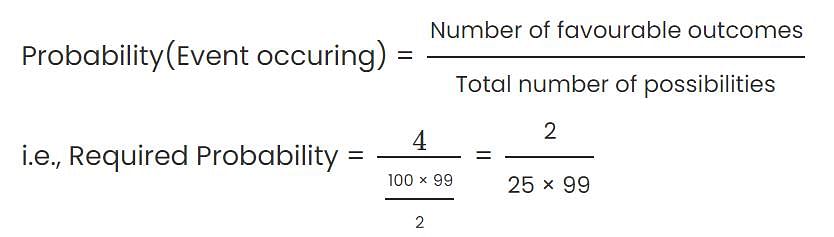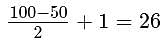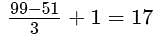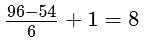Test: Quantitative Reasoning (Level 700) - 1 - GMAT MCQ
21 Questions MCQ Test - Test: Quantitative Reasoning (Level 700) - 1
A wholesaler purchases “n” mobile phones from the manufacturer at a price of $120 per mobile and sells them to the retailers at a price of $180 per mobile. Because the payments are made online, the wholesaler needs to pay a transaction charge of 5% while purchasing from the manufacturer and selling to the retailer. What is the profit percentage of the wholesaler after purchasing and selling all the “n” mobile phones?
In how many ways can the letters of the word "COMPUTER" be arranged if vowels occupy the even positions?
At a metal rolling factory, if a iron bar of square cross-section with an area of 4 square foot is moving continuously through a belt conveyor at a constant speed of 360 feet per hour, how many seconds does it take for a volume of 8.4 cubic foot of the iron bar to move through the conveyor?
x and n are positive integers, such that 7x = 10n–1. What is the 99th smallest possible value of n?
A box contains 100 balls, numbered from 1 to 100. If three balls are selected at random and with replacement from the box, what is the probability that the sum of the three numbers on the balls selected from the box will be odd?
A tea shop offers tea in cups of three different sizes. The product of the prices (in $) of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by $ 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes (in $) will be
Operating at the same time at their respective constant rates, Misha and Petro can repair 100 widgets in q hours. Working by himself at his constant rate, Misha repairs 100 widgets in w hours. In terms of q and w, how many hours does it take Petro, working alone at his constant rate, to repair 100 widgets?
A filled vessel contains 3 parts of water and 5 parts of syrup. How much of the mixture must be drawn out and replaced with water, so that the mixture has 50% water and 50% syrup ?
If y is the highest power of a number 'x' that can divide 101! without leaving a remainder, then for which among the following values of x will y be the highest?
A trader cheats both his supplier and customer by using faulty weights. When he buys from the supplier, he takes 10% more than the indicated weight. When he sells to his customer, he gives the customer a weight such that 10% of that is added to the weight, the weight claimed by the trader is obtained. If he charges the cost price of the weight that he claims, find his profit percentage.
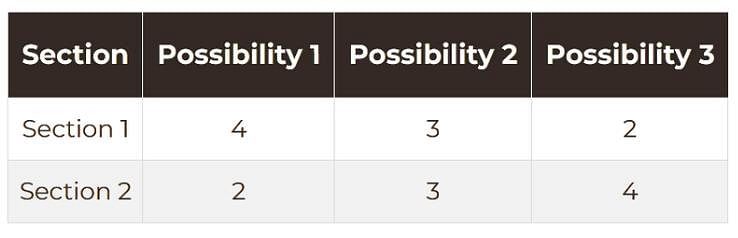
A student is required to solve 6 out of the 10 questions in a test. The questions are divided into two sections of 5 questions each. In how many ways can the student select the questions to solve if not more than 4 questions can be chosen from either section?
In Country C, the unemployment rate among construction workers dropped from 16 percent on September 1, 1992, to 9 percent on September 1, 1996. If the number of construction workers was 20 percent greater on September 1, 1996, than on September 1, 1992, what was the approximate percent change in the number of unemployed construction workers over this period?
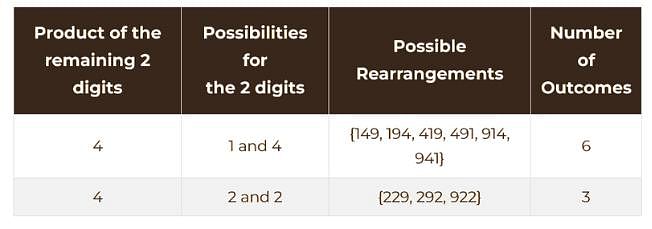
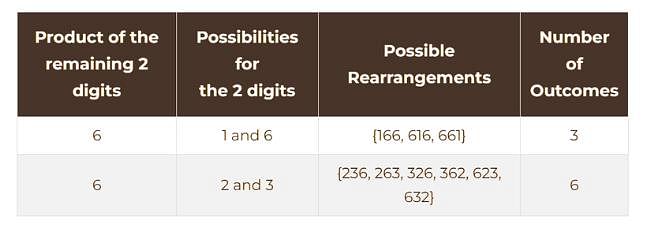
149 is a 3-digit positive integer, product of whose digits is 1 × 4 × 9 = 36. How many 3-digit positive integers exist, product of whose digits is 36?
John and Ingrid pay 30% and 40% tax annually, respectively. If John makes $56000 and Ingrid makes $72000, what is their combined tax rate?
If two distinct integers a and b are picked from {1, 2, 3, 4, .... 100} and multiplied, what is the probability that the resulting number has EXACTLY 3 factors ?
If a, b, and c are not equal to zero, what is the difference between the maximum and minimum value of S?
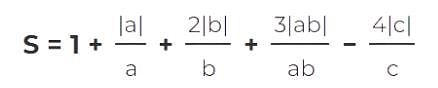
When positive integer a is divided by positive integer b, yielding quotient q and remainder r, the result is 5.125. Which of the following must be true?
What is the next number in the sequence: 2, 6, 22, 56, 114?
How many integers between 50 and 100, inclusive, are divisible by 2 or 3?
A nation’s population triples every 100 years. If the population was 100,000 in the year 1200, in what year was the population 72,900,000?
One night a certain hotel rented 3/4 of its rooms, including 2/3 of their air conditioned rooms. If 3/5 of its rooms were air conditioned, what percent of the rooms that were not rented were air conditioned?



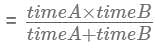 , where time for Misha = w, combined time = q and time for Petro = x.
, where time for Misha = w, combined time = q and time for Petro = x.