Test: Quantitative Reasoning (Level 600) - 1 - GMAT MCQ
21 Questions MCQ Test - Test: Quantitative Reasoning (Level 600) - 1
It takes three laborers ten hours to install four faucets (each faucet takes the same amount of work to install). How many hours would it take nine laborers to install twelve faucets?
Two hoses (A and B) are filling a pool. Working alone at their individual constant rates Hose A could fill the pool in 6 hours, and Hose B could do it in 4 hours. If Hose A works alone for one hour and then Hose B joins after that, how long will it take in total for the pool to be filled?
Working together, A and B can do a job in 6 days. B and C can do the same job in 10 days, while C and A can do it in 7.5 days. How long will it take if all A, B and C work together to complete the job?
There were 5 candidates (Alexa, Bill, Charlie, Dan, and Ernie) vying for student council, and 100 total votes were cast. Everyone received at least one vote, and no two candidates received the same number of votes. Alexa won the election with 40 votes, Bill came in 2nd, Charlie in 3rd, Dan in 4th, and Ernie in last. What is the greatest number of votes that Dan could have received?
A certain telephone company offers two plans, A and B. Under plan A, the company charges a total of $0.60 for the first 7 minutes of each call and $0.06 per minute thereafter. Under plan B, the company charges $0.08 per minute of each call. What is the duration of a call, in minutes, for which the company charges the same amount under plan A and under plan B?
There are 7 keys in a key ring. If two more keys are to be added in the ring at random, what is the probability that two keys will be adjacent?
A positive integer n is a perfect number provided that the sum of all the positive factors of n, including 1 and n, is equal to 2n. What is the sum of the reciprocals of all the positive factors of the perfect number 28?
The age of a group of people follows a distribution, which is symmetric about the average (mean) A. If 95% of the distribution falls within two standard deviation (SD) of the mean, then what percentage of the same distribution is less than A + 2SD?
For which of the following values of x is the units digit of the product 2*3x equal to 4?
If x and y are both odd prime numbers and x < y, how many distinct positive integer factors does 2xy have?
If the remainder is 5 when x is divided by 101, what is the remainder when x3+x2+x is divided by 101?
The positive integers m and n leave remainders of 2 and 3, respectively, when divided by 6. m > n.
What is the remainder when m – n is divided by 6?
How many integers from 1 to 1000, inclusive, have the same remainder when divided by 2, 3, 5, 7?
Children who ride the roller coaster must be between 24 and 52 inches tall. If x represents the height in inches of a child who may ride the roller coaster, which of the following absolute value inequalities represents all possible values of x?
If x < y, which of the following must be true?
On segment WZ above, if WY = 21, XZ = 26, and YZ is twice WX, what is the value of XY?
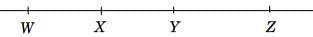

Which of the following is closest to the number of males who were not enrolled in college in 1993?
If s and t are integers greater than 1 and each is a factor of the integer n, which of the following must be a factor of nst ?
I. st
II. (st)2
III. s+t
Along a yard 225 metres long , 26 trees are planted at equal distance, one tree being at each end of the yard.What is the distance between two consecutive trees?
If K is the sum of the reciprocals of the consecutive integers from 43 to 48, inclusive, then K is closest in value to which of the following?
20% ammonia solution and 70% ammonia solution were mixed to form 50% ammonia solution. If 120 litres of 20% ammonia solution were used in the process, what was the volume of the 50% ammonia solution that was produced?




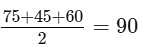
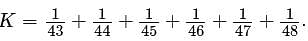 Notice that 1/43 is the larges term and 1/48 is the smallest term.
Notice that 1/43 is the larges term and 1/48 is the smallest term.














