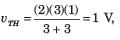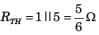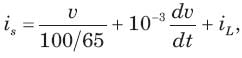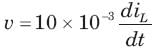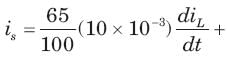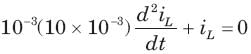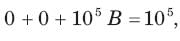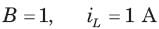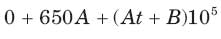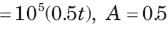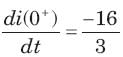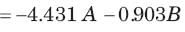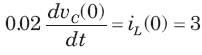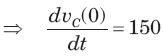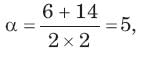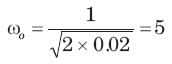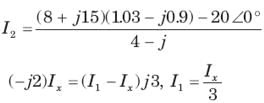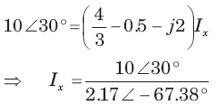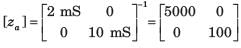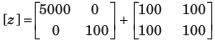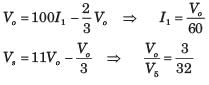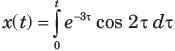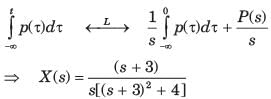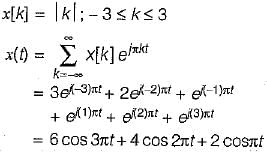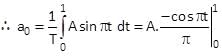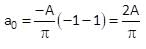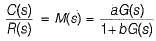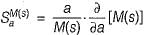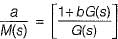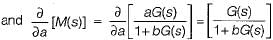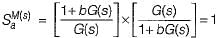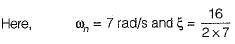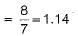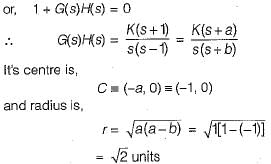Test: ESE Electrical - 5 - Electrical Engineering (EE) MCQ
30 Questions MCQ Test - Test: ESE Electrical - 5
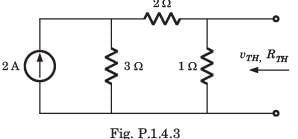
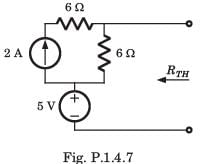
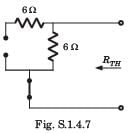
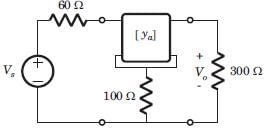
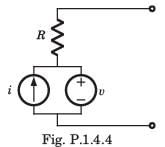
A simple equivalent circuit of the 2 terminal network shown in fig. P1.4.4 is

In the circuit shown in fig.all initial condition are zero.
If is (t) = 1 A, then the inductor current iL(t) is
In the circuit shown in fig. all initialcondition are zero
If is(t) = 0.5t A, then iL(t) is
In the circuit of fig. switch is moved from position a to b at t = 0. The iL(t) for t > 0 is
A 415 V, three-phase star-connected alternator supplies a delta-connected load, each phase of which has an impedance of (86∠54.46°) Ω. Calculate kVA rating of the alternator, neglecting losses in the line between the alternator and load.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the Y phase.
Two small diameter 10gm dielectric balls can slide freely on a vertical channel. Each carry a negative charge of 1μC. Find the separation between the balls if the lower ball is restrained from moving.
A charge of 2 X 10-7 C is acted upon by a force of 0.1N. Determine the distance to the other charge of 4.5 X 10-7 C, both the charges are in vacuum.
A control system transfer function is H(s) = 1/s3. Express its impulse response in terms of unit step signal
What is the inverse z-transform of X(z)=1/(1-1.5z-1+0.5z-2) if ROC is |z|>1?
Determine the bilateral laplace transform and choose correct option.
The Fourier series coefficient of time domain signal have been given. Determine the corresponding time domain signal and choose correct option.
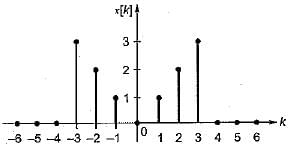
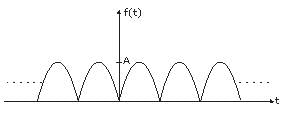
Determine the Fourier series coefficient for given periodic signal x(t).
x(t) as shown in fig.
A continuous-time signal has frequency content at f = 10 MHz, 50 MHz, and 70 MHz. The signal is sampled at a sampling frequency of 56 MHz and is then passed through a low-pass filter with a cutoff frequency of 15 MHz. The frequency content of the output of the filter will be:
How many complex additions are required to be performed in linear filtering of a sequence using FFT algorithm?
What is the approximate transition width of main lobe of a Hamming window?
What is the Fourier transform of the rectangular window of length M-1?
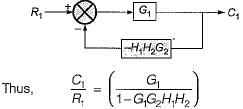
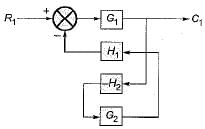
In the system shown in figure below, the sensitivity of the closed loop transfer function w.r.t. parameter a is

The value of for the system described by the block diagram shown in figure below Is.
A linear second-order system with the transfer function G(s) = 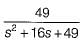 is initially at rest and is subjected to a step input signal.
is initially at rest and is subjected to a step input signal.
The response of the system will exhibit a peak overshoot of
Which one of the following is not a property of the Liapunov function?
The root locus of s(s - 1) + K(s + 1) = 0 is a circle. The co-ordinates of the centre and the radius (in units) of this circle are respectively
A system with phase margin close to zero or gain margin close to unity is