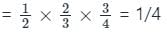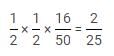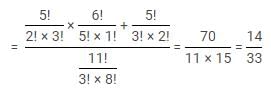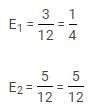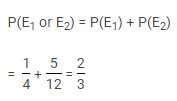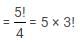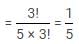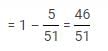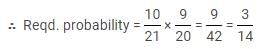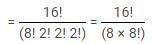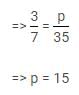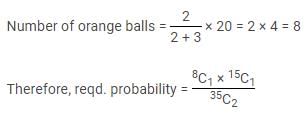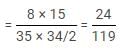MCQ Test: Probability- 1 - Bank Exams MCQ
20 Questions MCQ Test - MCQ Test: Probability- 1
A school has 4 clubs A, B, C and D. IX class has 30 students. Its 6 students are in club A, 7 in club B, 2 in club C and rest in D. A single student is selected at random from the class to act as class monitor. The probability that the selected student is from club A or D is:
Two unbiased dice are rolled simultaneously. Find the probability of getting sum greater than 5.
Probability of 3 students solving a question are 1/2,1/3,1/4. Probability to solve the question is:
The names of 5 students from section A, 6 students from section B and 7 students from section C were selected. The age of all the 18 students was different. Again, one name was selected from them and it was found that it was of section B. What was the probability that it was the youngest student of the section B?
A box contains slips with numbers from 1 to 50 written on them. A slip is drawn and replaced. Then another slip is drawn and after replacing another slip is drawn. What is the probability that an even number appears on the first draw, an odd number on the second draw and a number divisible by 3 on the third draw?
All the red face cards are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. The probability that the card drawn is a face card is :
A committee of 3 members is to be made out of 6 men and 5 women. What is the probability that the committee has at least two women?
There are 3 green, 4 orange and 5 white color bulbs in a bag. If a bulb is picked at random, what is the probability of having either a green or a white bulb?
A child paints the six faces of a cube with six different colors red, blue, pink, yellow, green and orange. What is the probability that red, pink and blue faces share a common corner?
There are total 18 balls in a bag. Out of them 6 are red in colour, 4 are green in colour and 8 are blue in colour. If Vishal picks three balls randomly from the bag, then what will be the probability that all the three balls are not of the same colour?
A box contains discs numbered from 10 to 90. If one disc is drawn at random from the box, the probability that number on disc is prime number and both digits of the number are also prime numbers, is :
A box contains 21 balls numbered 1 to 21. A ball is drawn and then another ball is drawn without replacement. What is the probability that both balls are even numbered?
Ram and Shyam are playing chess together. Ram knows the two rows in which he has to put all the pieces in but he doesn’t know how to place them. What is the probability that he puts all the pieces in the right place?
From the month of July, whose first day is Monday, a day is selected at random. The probability that it is not a Monday is :
A bag contains 35 balls of three different colors viz. red, orange and pink. The ratio of red balls to orange balls is 3 : 2, respectively and probability of choosing a pink ball is 3/7. If two balls are picked from the bag, then what is the probability that one ball is orange and one ball is pink?
A biased dice was rolled 600 times. The frequencies of the various outcomes are given in the following table :
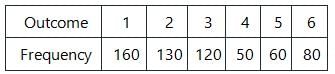
Now the dice is rolled once, the probability of getting a number which is a perfect square is :
When 4 fair coins are tossed together what is the probability of getting at least 3 heads?
The probability of Sita, Gita and Mita passing a test is 60%, 40% and 20% respectively. What is the probability that at Sita and Gita will pass the test and Mita will not?
Ajay rolled two dice together. What is the probability that first dice showed a multiple of 3 and the second dice showed an even number?