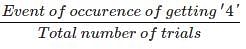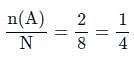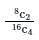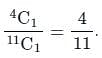MCQ Test: Experimental Probability - 1 - Banking Exams MCQ
20 Questions MCQ Test - MCQ Test: Experimental Probability - 1
1500 drivers were selected for a study to find a relationship between age and accidents. The data is shown in the table below.

What is the probability of being 35-50 years of age and having more no accidents?

What is the probability of being 35-50 years of age and having more no accidents?
1500 drivers were selected for a study to find a relationship between age and accidents. The data is shown in the table below.

What is the probability of being elder than 35 years of age and having at least one accident?

What is the probability of being elder than 35 years of age and having at least one accident?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
1500 drivers were selected for a study to find a relationship between age and accidents. The data is shown in the table below.

What is the probability of being 18-35 years of age and having more than 1 accidents?

What is the probability of being 18-35 years of age and having more than 1 accidents?
1000 families with 2 children were studied and the following data was collected.

What is the probability that the family has at least one boy?
Marks obtained by a student in a test is shown in the table below.

What is the probability that the student has scored more than 80?
A dice was thrown 500 times. Frequencies for the outcomes 1, 2, 3, 4, 5, and 6 are given in the table.

What is the probability of getting ‘4’ as outcome?
Two coins were tossed 200 times and the following results were obtained.
Two heads: 55
One head and one tail: 105
Two tails: 40
What is the probability of event of obtaining minimum one head?
From a pack of playing card, one card is drawn randomly. What is the probability that the card is red color or king?
What is the probability of getting a sum of 7 with two dice?
A coin is tossed 3 times. The probability of getting a head and a tail alternately is:
If four dice are thrown together, then what is the probability that the sum of the numbers appearing on them is 25?
The number of possible outcomes, when a coin is tossed 6 times, is
An unbiased coin is tossed 3 times, if the third toss gets head what is the probability of getting at least one more head?
In a room there are eight couples. Out of them if 4 people are selected at random, the probability that they may be couples is
Three mangoes and three apples are in box. If two fruits are chosen at random, the probability that one is a mango and the other is an apple is
A and B are two events such that P(B) = 0.4 and P(A ∪ B) = 0.6 If A and B are independent, then P(A) is
A bag contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. The probability of getting the balls of different colors is:
What is the probability of rolling a sum of 7 on two fair dice?
If events A and B are independent, what is the probability of A and B happening?
A biased coin with the probability of getting head equal to 1/4 is tossed five times. What is the probability of getting tail in all the first four tosses followed by head?


 = 0.73
= 0.73