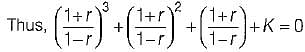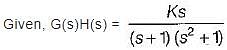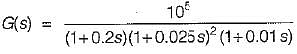Test: ESE Electrical - 10 - Electrical Engineering (EE) MCQ
30 Questions MCQ Test - Test: ESE Electrical - 10
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In superposition theorem, when we consider the effect of one current source, all the other current sources are____________
In A parallel circuit, with any number of impedances, The voltage across each impedance is?
In a parallel circuit, we consider _____________ instead of impedance.
A relay coil is connected to a 210 V, 50 Hz supply. If it has resistance of 30Ω and an inductance of 0.5 H, the apparent power is
For a 2-port symmetrical bilateral network, iftransmission parameters A = 3 and B = 1Ω , the value ofparameter C is
The voltage between ______________ is called line voltage.
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Determine the phase current IR.
Find the force due to a current element of length 2cm and flux density of 12 tesla. The current through the element will be 5A.
Let x1(t) and x2(t) be periodic signals with fundamental periods T1 and T2 respectively. Which of the following must be a rational number for x(t)=x1(t)+x2(t) to be periodic?
If X(z) has M finite zeros and N finite poles, then which of the following condition is true?
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 
Determine the Fourier series coefficient for given periodic signal x(t).
Q. x(t) = sin2t
The Fourier series of an odd periodic function, contains only
Select one:
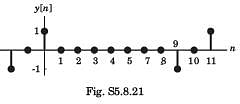
Consider a discrete-time periodic signal
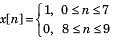
with period N = 10. Also y[n] = x[n] - x[n - 1]
Q. The fundamental period of y[n] is
To reduce side lobes, in which region of the filter the frequency specifications has to be optimized?
For a decimation-in-time FFT algorithm, which of the following is true?
What is the expression for cutoff frequency in terms of pass band gain?
The DC gain of the system represented by the following transfer function is
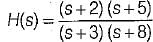
The signal flow graph shown below has M number of forward path and N number of individual loops.

Q. What are the values of M and N ?
Assertion (A): With the increase in bandwidth of the system the response of the system becomes fast.
Reason (R): Damping ratio of the system decreases with the increase in bandwidth.
The characteristic equation of a linear discrete-data control system is given as:
F(z) = z3 + z2 + z + K = 0,
Where K is a real constant.
What is the range of values of K so that the system is stable?
For the loop transfer function:

the angle of departure at s = j for K > 0 is
The magnitude plot of the open loop transfer function G(s) of a certain system is shown in figure below.
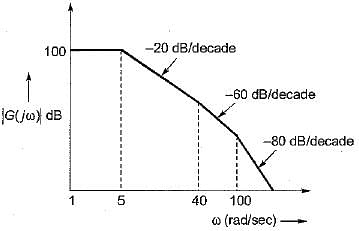
If the system is of minimum phase type, then the open-loop transfer function G(s) will be given by:


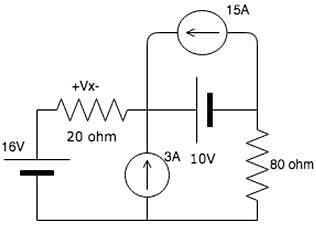

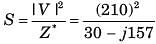
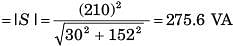

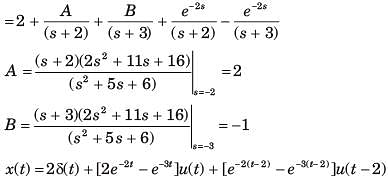



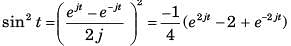
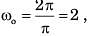
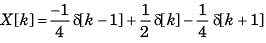
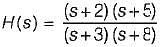
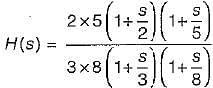
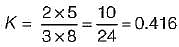
 in the above characteristic equation.
in the above characteristic equation.