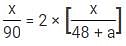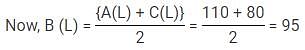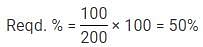All Courses
Get the App Signup / Login
Sign in Open App
Banking Exams Exam  >  Banking Exams Tests  >  MCQ Test: Caselets - 2 - Banking Exams MCQ

MCQ Test: Caselets - 2 - Banking Exams MCQ


Test Description

20 Questions MCQ Test - MCQ Test: Caselets - 2

MCQ Test: Caselets - 2 for Banking Exams 2024 is part of Banking Exams preparation. The MCQ Test: Caselets - 2 questions and answers have been prepared according to the Banking Exams exam syllabus.The MCQ Test: Caselets - 2 MCQs are made for Banking Exams 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ Test: Caselets - 2 below.
Solutions of MCQ Test: Caselets - 2 questions in English are available as part of our course for Banking Exams & MCQ Test: Caselets - 2 solutions in Hindi for Banking Exams course. Download more important topics, notes, lectures and mock test series for Banking Exams Exam by signing up for free. Attempt MCQ Test: Caselets - 2 | 20 questions in 20 minutes | Mock test for Banking Exams preparation | Free important questions MCQ to study for Banking Exams Exam | Download free PDF with solutions
MCQ Test: Caselets - 2 - Question 1
Save

Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].

Q. What should come in place of A?

Detailed Solution for MCQ Test: Caselets - 2 - Question 1

Let the speed of the vulture be a km/hr
Relative speed of A and B = (42 + 48) = 90 km/hr
Relative speed of vulture and B (when vulture approaches B) = a + 48
Given: Vulture reaches B in half time as A from the point vulture starts
Let x be the distance travelled

180 = 48 + a
a = 132 km/hr (Blank B)
Distance between B’s meeting point with vulture and A is 72
Time taken by B = 72/48 = 1.5 hours
This 1.5 hour will be half the time as Vulture reaches B in half time as A from the point vulture starts
So, total times for A to meet B (from the point when Vulture started) = 2 × 1.5 = 3 hours
Hence total meeting time = 3 + 12/60 = 3.2 hours
Distance (blank A) = 3.2 × (48 + 42) = 288 km

Hence, option C is correct.

MCQ Test: Caselets - 2 - Question 2
Save

Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].

Q. What should come in place of C?

Detailed Solution for MCQ Test: Caselets - 2 - Question 2

Let speed of the vulture be a km/hr
Relative speed of A and B = (42 + 48) = 90 km/hr
Relative speed of vulture and B (when vulture approaches B) = a + 48
Given: Vulture reaches B in half time as A from the point vulture starts
Let x be the distance travelled

180 = 48 + a
a = 132 km/hr (Blank B)
Distance between B’s meeting point with vulture and A is 72
Time taken by B = 72/48 = 1.5 hours
This 1.5 hour will be half the time as Vulture reaches B in half time as A from the point vulture starts
So, total times for A to meet B (from the point when Vulture started) = 2 × 1.5 = 3 hours

Distance travelled by vulture = 132 × 3 = 396 km (Blank C)

Hence, option D is correct.

1 Crore+ students have signed up on EduRev. Have you? Download the App
MCQ Test: Caselets - 2 - Question 3
Save

Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].

Q. What will come in place of B?

Detailed Solution for MCQ Test: Caselets - 2 - Question 3

Let speed of vulture be a km/hr
Relative speed of A and B = (42 + 48) = 90 km/hr
Relative speed of vulture and B (when vulture approaches B) = a + 48
Given: Vulture reaches B in half time as A from the point vulture starts
Let x be the distance travelled

180 = 48 + a
a = 132 km/hr (Blank B)
Hence, option E is correct.

MCQ Test: Caselets - 2 - Question 4
Save

Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].

Q. What should come in place of D?
Detailed Solution for MCQ Test: Caselets - 2 - Question 4

Let the speed of the vulture be a km/hr
Relative speed of A and B = (42 + 48) = 90 km/hr
Relative speed of vulture and B (when vulture approaches B) = a + 48
Given: Vulture reaches B in half time as A from the point vulture starts
Let x be the distance travelled

180 = 48 + a
a = 132 km/hr (Blank B)
Distance between B’s meeting point with vulture and A is 72
Time taken by B = 72/48 = 1.5 hours
This 1.5 hour will be half the time as Vulture reaches B in half time as A from the point vulture starts
So, total times for A to meet B (from the point when Vulture started) = 2 × 1.5 = 3 hours
Distance travelled by vulture = 132 × 3 = 396 km (Blank C)
Distance between A and B (when vulture starts) = 3 × (48 + 42) = 270 km
Vulture meets B in 1.5 hours (given)
Distance between A and B when Vulture meets B for the first time = (3 – 1.5) × (48 + 42) = 135
Time taken by Vulture to reach till A

Distance between A and B when Vulture meets A (after return)

Time taken for vulture to travel 65.2 (to meet B for second time)


Distance (Blank D) = 65.2 –
Hence, option B is correct.

MCQ Test: Caselets - 2 - Question 5
Save

Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.

The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.

Q. What is the ratio of amount spent by Aman on breakfast and dinner to the amount spent by Chintu on breakfast and dinner?
Detailed Solution for MCQ Test: Caselets - 2 - Question 5

Following the common explanation, we get
Aman (B + D) = Rs. (60 +140) = Rs. 200
Chintu (B + D) = Rs. (140 + 70) = Rs. 210
Ratio = 20 : 21
Hence, Option D is correct.

Common explanation : 
Aman (Breakfast) = A (B); Aman (Lunch) = A (L),and likewise for Binoy and Chintu
A (B) : A (L) = 3 : 4 (7units)
C (L) : C (D) = 11 : 7 (18 units)
A (B) + A (L) = 77 7/9 % {C(L) + C(D)}

A (B) + A (L) = 14k → A (B) = 6k; A (L) = 8k

C (L) + C (D) = 18k → C (L) = 11k ; C (D) = 7k

As A (D) = C (B), Difference between amount of A and C will be

C (L) + C(D) – A(B) – A(L) = 18k – 14k = 4k

As Aman gives Rs. 20 to Chintu to make the contribution of all three equal, the original difference between them must have been Rs 40.

So, 4k = 40 → k=10

A (B) = 6k = 60, A (L) = 8k = 80

C (L) = 11k = 110, C (D) = 70

Total lunch = A (L) + B (L) + C (L) = 80 + 95 + 110 = 285

Breakfast: Lunch: Dinner = 58 : 57 : 65

If Lunch (57units) = 285 → Breakfast (58 units) = 290 & Dinner (65 units) = 325

Total = 285 + 290 + 325 = 900

Contribution of them becomes equal after Aman gives Chintu Rs. 20, so contribution of Aman previously was Rs. 20 less and that of chintu was Rs. 20 more than the average contribution of all three (which is 900/3 = 300).

So, Aman + 20  = Binoy = Chintu - 20 = 900/3 = 300

So, Aman = 300 - 20 = 280, Binoy =  300 and Chintu = 300 + 20 = 320

Aman(D) = 280 - 60 - 80 = 140

So A(D) = C(B) = 140

MCQ Test: Caselets - 2 - Question 6
Save

Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.

The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.

Q. What is the difference between the total amount spent on breakfast and dinner?
Detailed Solution for MCQ Test: Caselets - 2 - Question 6

Following the common explanation, we get
Dinner – breakfast = 325 – 90 = Rs. 35
Hence, Option E is correct.

Common explanation : 
Aman (Breakfast) = A (B); Aman (Lunch) = A (L),and likewise for Binoy and Chintu
A (B) : A (L) = 3 : 4 (7units)
C (L) : C (D) = 11 : 7 (18 units)
A (B) + A (L) = 77 7/9 % {C(L) + C(D)}

A (B) + A (L) = 14k → A (B) = 6k; A (L) = 8k

C (L) + C (D) = 18k → C (L) = 11k ; C (D) = 7k

As A (D) = C (B), Difference between amount of A and C will be

C (L) + C(D) – A(B) – A(L) = 18k – 14k = 4k

As Aman gives Rs. 20 to Chintu to make the contribution of all three equal, the original difference between them must have been Rs 40.

So, 4k = 40 → k=10

A (B) = 6k = 60, A (L) = 8k = 80

C (L) = 11k = 110, C (D) = 70

Total lunch = A (L) + B (L) + C (L) = 80 + 95 + 110 = 285

Breakfast: Lunch: Dinner = 58 : 57 : 65

If Lunch (57units) = 285 → Breakfast (58 units) = 290 & Dinner (65 units) = 325

Total = 285 + 290 + 325 = 900

Contribution of them becomes equal after Aman gives Chintu Rs. 20, so contribution of Aman previously was Rs. 20 less and that of chintu was Rs. 20 more than the average contribution of all three (which is 900/3 = 300).

So, Aman + 20  = Binoy = Chintu - 20 = 900/3 = 300

So, Aman = 300 - 20 = 280, Binoy =  300 and Chintu = 300 + 20 = 320

Aman(D) = 280 - 60 - 80 = 140

So A(D) = C(B) = 140

MCQ Test: Caselets - 2 - Question 7
Save

Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.

The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.

Q. What would have been the ratio of total amount spent by Aman and Binoy, had they split the dinner amount paid by Chintu between them evenly?
Detailed Solution for MCQ Test: Caselets - 2 - Question 7

From common explanation, we have
Chintu(dinner) = 70
If equally split between Aman and Binoy
Aman = 280 + 35 = 315; Binoy = 300 + 35 = 335
Ratio = 315 : 335 = 63 : 67
Hence, Option C is correct.

Common explanation : 
Aman (Breakfast) = A (B); Aman (Lunch) = A (L),and likewise for Binoy and Chintu
A (B) : A (L) = 3 : 4 (7units)
C (L) : C (D) = 11 : 7 (18 units)
A (B) + A (L) = 77 7/9 % {C(L) + C(D)}

A (B) + A (L) = 14k → A (B) = 6k; A (L) = 8k

C (L) + C (D) = 18k → C (L) = 11k ; C (D) = 7k

As A (D) = C (B), Difference between amount of A and C will be

C (L) + C(D) – A(B) – A(L) = 18k – 14k = 4k

As Aman gives Rs. 20 to Chintu to make the contribution of all three equal, the original difference between them must have been Rs 40.

So, 4k = 40 → k=10

A (B) = 6k = 60, A (L) = 8k = 80

C (L) = 11k = 110, C (D) = 70

Total lunch = A (L) + B (L) + C (L) = 80 + 95 + 110 = 285

Breakfast: Lunch: Dinner = 58 : 57 : 65

If Lunch (57units) = 285 → Breakfast (58 units) = 290 & Dinner (65 units) = 325

Total = 285 + 290 + 325 = 900

Contribution of them becomes equal after Aman gives Chintu Rs. 20, so contribution of Aman previously was Rs. 20 less and that of chintu was Rs. 20 more than the average contribution of all three (which is 900/3 = 300).

So, Aman + 20  = Binoy = Chintu - 20 = 900/3 = 300

So, Aman = 300 - 20 = 280, Binoy =  300 and Chintu = 300 + 20 = 320

Aman(D) = 280 - 60 - 80 = 140

So A(D) = C(B) = 140

MCQ Test: Caselets - 2 - Question 8
Save

Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.

The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.

Q. The amount spent on dinner by Binoy is what percent of the total amount spent by him?
Detailed Solution for MCQ Test: Caselets - 2 - Question 8

Following the common explanation, we get
Amount spent by Binoy(dinner) = Rs. 115
Total amount spent by Binoy = Rs. 300
As percent = 115/300 × 100 = 38.33%
Hence, option A is correct.

Common explanation : 
Aman (Breakfast) = A (B); Aman (Lunch) = A (L),and likewise for Binoy and Chintu
A (B) : A (L) = 3 : 4 (7units)
C (L) : C (D) = 11 : 7 (18 units)
A (B) + A (L) = 77 7/9 % {C(L) + C(D)}

A (B) + A (L) = 14k → A (B) = 6k; A (L) = 8k

C (L) + C (D) = 18k → C (L) = 11k ; C (D) = 7k

As A (D) = C (B), Difference between amount of A and C will be

C (L) + C(D) – A(B) – A(L) = 18k – 14k = 4k

As Aman gives Rs. 20 to Chintu to make the contribution of all three equal, the original difference between them must have been Rs 40.

So, 4k = 40 → k=10

A (B) = 6k = 60, A (L) = 8k = 80

C (L) = 11k = 110, C (D) = 70

Total lunch = A (L) + B (L) + C (L) = 80 + 95 + 110 = 285

Breakfast: Lunch: Dinner = 58 : 57 : 65

If Lunch (57units) = 285 → Breakfast (58 units) = 290 & Dinner (65 units) = 325

Total = 285 + 290 + 325 = 900

Contribution of them becomes equal after Aman gives Chintu Rs. 20, so contribution of Aman previously was Rs. 20 less and that of chintu was Rs. 20 more than the average contribution of all three (which is 900/3 = 300).

So, Aman + 20  = Binoy = Chintu - 20 = 900/3 = 300

So, Aman = 300 - 20 = 280, Binoy =  300 and Chintu = 300 + 20 = 320

Aman(D) = 280 - 60 - 80 = 140

So A(D) = C(B) = 140

MCQ Test: Caselets - 2 - Question 9
Save

Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.

The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.

Q. The amount spent by Aman on breakfast, Binoy on lunch and Chintu on dinner is what percent of the total expenditure of all three?
Detailed Solution for MCQ Test: Caselets - 2 - Question 9

From a common explanation, we have
A (B) + B (L) + C (D) = 60 + 95 + 70 = 225
As a percent of total = 225/900 × 100 = 25%
Hence, Option D is correct.

Common explanation : 
Aman (Breakfast) = A (B); Aman (Lunch) = A (L),and likewise for Binoy and Chintu
A (B) : A (L) = 3 : 4 (7units)
C (L) : C (D) = 11 : 7 (18 units)
A (B) + A (L) = 77 7/9 % {C(L) + C(D)}

A (B) + A (L) = 14k → A (B) = 6k; A (L) = 8k

C (L) + C (D) = 18k → C (L) = 11k ; C (D) = 7k

As A (D) = C (B), Difference between amount of A and C will be

C (L) + C(D) – A(B) – A(L) = 18k – 14k = 4k

As Aman gives Rs. 20 to Chintu to make the contribution of all three equal, the original difference between them must have been Rs 40.

So, 4k = 40 → k=10

A (B) = 6k = 60, A (L) = 8k = 80

C (L) = 11k = 110, C (D) = 70

Total lunch = A (L) + B (L) + C (L) = 80 + 95 + 110 = 285

Breakfast: Lunch: Dinner = 58 : 57 : 65

If Lunch (57units) = 285 → Breakfast (58 units) = 290 & Dinner (65 units) = 325

Total = 285 + 290 + 325 = 900

Contribution of them becomes equal after Aman gives Chintu Rs. 20, so contribution of Aman previously was Rs. 20 less and that of chintu was Rs. 20 more than the average contribution of all three (which is 900/3 = 300).

So, Aman + 20  = Binoy = Chintu - 20 = 900/3 = 300

So, Aman = 300 - 20 = 280, Binoy =  300 and Chintu = 300 + 20 = 320

Aman(D) = 280 - 60 - 80 = 140

So A(D) = C(B) = 140

MCQ Test: Caselets - 2 - Question 10
Save

Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website. 
Further it is known that 

  1. Total number of hotels listed on all three website together is 720. 
  2. Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together. 
  3. Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
  4. Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
  5. Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website. 
  6. Number of 3 star hotels on website B and C are same. 

Q. 4 Star Hotels on Site B is what percent of total number Hotels on Site A ?
Detailed Solution for MCQ Test: Caselets - 2 - Question 10

Following the common explanation, we get
4 Star Hotels on Site B = 100
Total Hotels on Site A = 200

Hence, option E is correct.

Common explanation :
It is given that total number of hotels is 720. 
4 star hotels = 2 × (3 star hotels)
5 star hotels = 3 × (4 star hotels)
Let, 3 star hotels M, 4 star hotels N and 5 star hotels P. 
N = 2M
P = 3N
M + 2M + 6M = 720
9M = 720
M = 80
N = 160
P = 480
Total 200 hotels listed on sites A. Out of which, 30% are 3 star.
60 hotels are there in 3 star category on Site A. 
Total 5 star hotels are 480. 
Ratio of the hotels on site A, B and C is 1:1:2. 
4x = 480
x = 120
Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
Number of 5 Star Hotels on site B = 120 
So, number of 4 star hotels on site B would be 100. 
Total 4 star hotels are 160.
So 4 star hotels on site C will be 160 – 20 – 100 = 40
Number of 3 star hotels on website B and C are same. 
Total 80
 
So 3 star and 4 star hotels on site B and C should be 10. 

MCQ Test: Caselets - 2 - Question 11
Save

Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website. 
Further it is known that 

  1. Total number of hotels listed on all three website together is 720. 
  2. Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together. 
  3. Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
  4. Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
  5. Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website. 
  6. Number of 3 star hotels on website B and C are same. 

Q. What is the total number of 4 star hotels from website A and C together ? 
Detailed Solution for MCQ Test: Caselets - 2 - Question 11

Following the common explanation, we get
Total number of 4 star hotels from Site A and C together are 60
Hence, option C is correct.

Common explanation :
It is given that total number of hotels is 720. 
4 star hotels = 2 × (3 star hotels)
5 star hotels = 3 × (4 star hotels)
Let, 3 star hotels M, 4 star hotels N and 5 star hotels P. 
N = 2M
P = 3N
M + 2M + 6M = 720
9M = 720
M = 80
N = 160
P = 480
Total 200 hotels listed on sites A. Out of which, 30% are 3 star.
60 hotels are there in 3 star category on Site A. 
Total 5 star hotels are 480. 
Ratio of the hotels on site A, B and C is 1:1:2. 
4x = 480
x = 120
Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
Number of 5 Star Hotels on site B = 120 
So, number of 4 star hotels on site B would be 100. 
Total 4 star hotels are 160.
So 4 star hotels on site C will be 160 – 20 – 100 = 40
Number of 3 star hotels on website B and C are same. 
Total 80
 
So 3 star and 4 star hotels on site B and C should be 10. 

MCQ Test: Caselets - 2 - Question 12
Save

Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website. 
Further it is known that 

  1. Total number of hotels listed on all three website together is 720. 
  2. Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together. 
  3. Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
  4. Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
  5. Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website. 
  6. Number of 3 star hotels on website B and C are same. 

Q. Website D also started listing of Hotels on their site. Number of 3 star hotels on site D is 50% more than number of 4 star hotels on site A. Total number of hotels (3 star, 4 star and 5 star) on site D are 500, out of which 50% are 4 star. Find the number of 5 star hotels listed on site D. 
Detailed Solution for MCQ Test: Caselets - 2 - Question 12

Following the common explanation, we get
3 star hotels on site D is 50% more than number of 4 star hotels on site A
3 star hotels on Site D = 150% of 20 = 30
Total Hotels on site D = 500
Out of Which 50% are 4 star = 250
Number of 4 star hotels on site D = 500 – 250 – 30 = 220
Hence, option B is correct.

Common explanation :
It is given that total number of hotels is 720. 
4 star hotels = 2 × (3 star hotels)
5 star hotels = 3 × (4 star hotels)
Let, 3 star hotels M, 4 star hotels N and 5 star hotels P. 
N = 2M
P = 3N
M + 2M + 6M = 720
9M = 720
M = 80
N = 160
P = 480
Total 200 hotels listed on sites A. Out of which, 30% are 3 star.
60 hotels are there in 3 star category on Site A. 
Total 5 star hotels are 480. 
Ratio of the hotels on site A, B and C is 1:1:2. 
4x = 480
x = 120
Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
Number of 5 Star Hotels on site B = 120 
So, number of 4 star hotels on site B would be 100. 
Total 4 star hotels are 160.
So 4 star hotels on site C will be 160 – 20 – 100 = 40
Number of 3 star hotels on website B and C are same. 
Total 80
 
So 3 star and 4 star hotels on site B and C should be 10. 

MCQ Test: Caselets - 2 - Question 13
Save

Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website. 
Further it is known that 

  1. Total number of hotels listed on all three website together is 720. 
  2. Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together. 
  3. Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
  4. Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
  5. Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website. 
  6. Number of 3 star hotels on website B and C are same. 

Q. What is the difference between 3 star hotels on site A and 4 star hotels on site C ?
Detailed Solution for MCQ Test: Caselets - 2 - Question 13

Following the common explanation, we get
3 star Hotels on site A = 60
4 star Hotels on Site C = 40
Difference = 20
Hence, option A is correct.

Common explanation :
It is given that total number of hotels is 720. 
4 star hotels = 2 × (3 star hotels)
5 star hotels = 3 × (4 star hotels)
Let, 3 star hotels M, 4 star hotels N and 5 star hotels P. 
N = 2M
P = 3N
M + 2M + 6M = 720
9M = 720
M = 80
N = 160
P = 480
Total 200 hotels listed on sites A. Out of which, 30% are 3 star.
60 hotels are there in 3 star category on Site A. 
Total 5 star hotels are 480. 
Ratio of the hotels on site A, B and C is 1:1:2. 
4x = 480
x = 120
Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
Number of 5 Star Hotels on site B = 120 
So, number of 4 star hotels on site B would be 100. 
Total 4 star hotels are 160.
So 4 star hotels on site C will be 160 – 20 – 100 = 40
Number of 3 star hotels on website B and C are same. 
Total 80
 
So 3 star and 4 star hotels on site B and C should be 10. 

MCQ Test: Caselets - 2 - Question 14
Save

Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website. 
Further it is known that 

  1. Total number of hotels listed on all three website together is 720. 
  2. Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together. 
  3. Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
  4. Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
  5. Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website. 
  6. Number of 3 star hotels on website B and C are same. 

Q. What is the total number of Hotels listed on Website C ?
Detailed Solution for MCQ Test: Caselets - 2 - Question 14

Following the common explanation, we get
Total number of Hotels listed on site C is 290. 
Hence, option A is correct.

Common explanation :
It is given that total number of hotels is 720. 
4 star hotels = 2 × (3 star hotels)
5 star hotels = 3 × (4 star hotels)
Let, 3 star hotels M, 4 star hotels N and 5 star hotels P. 
N = 2M
P = 3N
M + 2M + 6M = 720
9M = 720
M = 80
N = 160
P = 480
Total 200 hotels listed on sites A. Out of which, 30% are 3 star.
60 hotels are there in 3 star category on Site A. 
Total 5 star hotels are 480. 
Ratio of the hotels on site A, B and C is 1:1:2. 
4x = 480
x = 120
Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
Number of 5 Star Hotels on site B = 120 
So, number of 4 star hotels on site B would be 100. 
Total 4 star hotels are 160.
So 4 star hotels on site C will be 160 – 20 – 100 = 40
Number of 3 star hotels on website B and C are same. 
Total 80
 
So 3 star and 4 star hotels on site B and C should be 10. 

MCQ Test: Caselets - 2 - Question 15
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. How much did the bank have to pay in total for two years on behalf of Natasha?
Detailed Solution for MCQ Test: Caselets - 2 - Question 15

Total expenditure on rent = 24 months × $550 = $13200
Total expenditure on utilities = 24 months × $340 = $8160
Total expenditure on tuition fees = 4 semesters × $25000 = $100000
Thus total expenditure = $(13200 + 8160 + 100000) = $121360
The bank paid 80% of this amount.
∴ Amount paid by the bank = (80/100) × 121360 = $97088
Hence, option C is correct.

MCQ Test: Caselets - 2 - Question 16
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. Find, the annual amount spent on utilities is what percentage less than the annual amount spent on rent? (Approximate)
Detailed Solution for MCQ Test: Caselets - 2 - Question 16

Total annual expenditure on rent = 12 months × $550 = $6600
Total annual expenditure on utilities = 12 months × $340 = $4080
Clearly the amount spent on utilities is less than the amount spent on rent
∴ Required percentage = [(6600 – 4080)/6600] × 100
= (2520 × 100)/6600 = 38. 18 = 38% (approximate)
Hence, option B is correct.

MCQ Test: Caselets - 2 - Question 17
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. Natasha decides to live with her relatives for 6 months so she will not have to pay for rent and utilities. How much does she save on rent and utilities?
Detailed Solution for MCQ Test: Caselets - 2 - Question 17

Per month rent = $550
Utilities cost per month = $340
∴ The amount she would save in 6 months = 6 × (550 + 340) = 6 × 890 = $5340
Hence, option C is correct.

MCQ Test: Caselets - 2 - Question 18
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. If the bank charges simple interest at the rate of 9% per annum, then find the total interest amount that Natasha paid after 2 years. (Assume she pays off the entire loan after 2 years of completion of course)
Detailed Solution for MCQ Test: Caselets - 2 - Question 18

Total expenditure on rent = 24 months × $550 = $13200
Total expenditure on utilities = 24 months × $340 = $8160
Total expenditure on tuition fees = 4 semesters × $25000 = $100000
Thus total expenditure = 13200 + 8160 + 100000 = $121360
The bank paid 80% of this amount.
∴ Amount paid by the bank = 80/100 × 121360 = $97088
Simple Interest = (97088 × 2 × 9)/100 = $17475. 84
Hence, option E is correct.

MCQ Test: Caselets - 2 - Question 19
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. Natasha gets an internship for a period of 3 months. The company where she'll be doing internship pays $12000 per month. The utilities and rent for these 3 months is what percentage of the total amount she earns from the internship?
Detailed Solution for MCQ Test: Caselets - 2 - Question 19

The salary earned during internship = 3 × 12000 = $36000
Total expenditure on rent in 3 months = 3 × $550 = $1650
Total expenditure on utilities in 3 months = 3 × $340 = $1020
Total expense = $(1650 + 1020) = $2670
∴ Required percentage = (2670/36000) × 100 = 267/36 = 7. 41
Hence, option A is correct.

MCQ Test: Caselets - 2 - Question 20
Save

Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.

Q. How much money did Natasha have to bear for her two-year course at MIT, considering the loan agreement guaranteed to pay 80% of all her expenses?
Detailed Solution for MCQ Test: Caselets - 2 - Question 20

To calculate the amount of money Natasha had to bear for her two-year course at MIT, we need to determine the total expenses for the course and then subtract 80% of those expenses, as per the loan agreement.

First, let's calculate the total expenses for two years:

Apartment rent per month = $550
Total rent for two years = $550/month * 12 months/year * 2 years = $13,200

Tuition fee for the current semester = $25,000

Utilities and groceries per month = $340
Total utilities and groceries for two years = $340/month * 12 months/year * 2 years = $8,160

Total expenses for two years = Rent + Tuition fee + Utilities/Groceries
Total expenses for two years = $13,200 + $25,000 + $8,160 = $46,360

According to the loan agreement, Natasha's loan covers 80% of her expenses. Therefore, the amount she has to bear is 20% of the total expenses:

Amount to bear = 20% * Total expenses
Amount to bear = 0.2 * $46,360
Amount to bear = $9,272

Therefore, Natasha had to bear $9,272 for her two-year course at MIT.

Information about MCQ Test: Caselets - 2 Page
In this test you can find the Exam questions for MCQ Test: Caselets - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for MCQ Test: Caselets - 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Banking Exams

Download as PDF

Top Courses for Banking Exams

Important Questions for MCQ Test: Caselets - 2

Find all the important questions for MCQ Test: Caselets - 2 at EduRev.Get fully prepared for MCQ Test: Caselets - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the MCQ Test: Caselets - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of MCQ Test: Caselets - 2 resources.

MCQ Test: Caselets - 2

Prepare for the MCQ Test: Caselets - 2 within the Banking Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for MCQ Test: Caselets - 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ Test: Caselets - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup