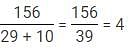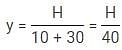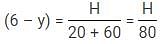All Courses
Get the App Signup / Login
Sign in Open App
Banking Exams Exam  >  Banking Exams Tests  >  MCQ Test: Caselets - 3 - Banking Exams MCQ

MCQ Test: Caselets - 3 - Banking Exams MCQ


Test Description

20 Questions MCQ Test - MCQ Test: Caselets - 3

MCQ Test: Caselets - 3 for Banking Exams 2024 is part of Banking Exams preparation. The MCQ Test: Caselets - 3 questions and answers have been prepared according to the Banking Exams exam syllabus.The MCQ Test: Caselets - 3 MCQs are made for Banking Exams 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ Test: Caselets - 3 below.
Solutions of MCQ Test: Caselets - 3 questions in English are available as part of our course for Banking Exams & MCQ Test: Caselets - 3 solutions in Hindi for Banking Exams course. Download more important topics, notes, lectures and mock test series for Banking Exams Exam by signing up for free. Attempt MCQ Test: Caselets - 3 | 20 questions in 20 minutes | Mock test for Banking Exams preparation | Free important questions MCQ to study for Banking Exams Exam | Download free PDF with solutions
MCQ Test: Caselets - 3 - Question 1
Save

Directions: Study the following information carefully and answer the questions given beside.
Mr. Dexter has four kids and all were born on same date of different years. They all have birthday today. Mr. Dexter wants to buy chocolates for all his kids. But he don’t want to give each kid equal number of chocolates.
He decides to do the following thing:
He will divide the height (in centimeters) by the sum of age number with weight (in kilogram).
He arrive at this formula –
Number of chocolate = height in centimeters/(weight in kilogram + age)
The number that will come is the number of chocolates that a particular kid gets.
His second youngest kid is twice the age of the youngest kid whose age is one-third the oldest kid. The second oldest kid is three year younger than the oldest kid. Weight of oldest kid is 36 kg which is numerically three times the age of second oldest kid, whose weight is four times the age of second youngest kid. Weight of the youngest kid is 40% less than the second oldest kid. Sum of weight of all four kids is 129 kg.

Q. After two years, weight of oldest kid increases 4 kg, second oldest kid by 2 kg, the second youngest kid gains 6kg and the youngest kid gains 9 kg weight. Ratio of average weight to average age of all the four kids.

Detailed Solution for MCQ Test: Caselets - 3 - Question 1

From common explanation we see weights after two years become:
36 + 4 = 40 kg
40 + 2 = 42 kg
29 + 6 = 35 kg
24 + 9 = 33 kg
Total = 150
Average weight = 150/4 kg
After 2 years, ages would be
(15 + 2), (12 + 2), (10 + 2), and (5 + 2)
17, 14, 12, and 7
Average age =

Hence, option C is correct.

Common explanation:
It is given that the second youngest kid is twice the age of the youngest kid whose age is three times less than the oldest kid.
Let the age of youngest kid is ‘y’, then the second youngest kid would be 2y and the oldest would be 3y.
Weight of oldest kid is 36 kg which is numerically three times more than the age of second oldest kid.
Age of second oldest kid would be 12 years. 
Since, the second oldest kid is three year younger than the oldest kid, oldest kid would be 15 years. From this we get 3y = 15, thus y = 3. So the age of youngest kid = 5 years, second youngest kid = 10 years.
Second oldest kid, whose weight is four times the age of second youngest kid
Second youngest kid = 10 years, so weight of second oldest kid = 4 × 10 = 40 kg
Weight of the youngest kid is 40% less than the second oldest kid
Weight of second oldest = 40kg, youngest kid = 40kg – 40% of 40kg = 24kg
Sum of all the weights = 129kg = 36kg + 24kg + 40kg + weight of second youngest kid
Weight of second youngest kid = 29kg

In a table form all the values are: 

MCQ Test: Caselets - 3 - Question 2
Save

Directions: Study the following information carefully and answer the questions given beside.
Mr. Dexter has four kids and all were born on same date of different years. They all have birthday today. Mr. Dexter wants to buy chocolates for all his kids. But he don’t want to give each kid equal number of chocolates.
He decides to do the following thing:
He will divide the height (in centimeters) by the sum of age number with weight (in kilogram).
He arrive at this formula –
Number of chocolate = height in centimeters/(weight in kilogram + age)
The number that will come is the number of chocolates that a particular kid gets.
His second youngest kid is twice the age of the youngest kid whose age is one-third the oldest kid. The second oldest kid is three year younger than the oldest kid. Weight of oldest kid is 36 kg which is numerically three times the age of second oldest kid, whose weight is four times the age of second youngest kid. Weight of the youngest kid is 40% less than the second oldest kid. Sum of weight of all four kids is 129 kg.

Q. How many total chocolates were distributed if oldest and second oldest got total 6 and the height of youngest is 145 cm while the second youngest is 11 cm taller than the youngest?

Detailed Solution for MCQ Test: Caselets - 3 - Question 2

From common explanation, we have

It is given the two of them got total of 6 chocolates.

Youngest kid’s height is 145 cm, so

Number of chocolate = 

Number of chocolate = 
Second youngest height = 145 + 11 = 156 cm
Number of chocolate = 
Total chocolates = 6 + 5 + 4 = 15
Hence, option D is correct.

Common explanation:
It is given that the second youngest kid is twice the age of the youngest kid whose age is three times less than the oldest kid.
Let the age of youngest kid is ‘y’, then the second youngest kid would be 2y and the oldest would be 3y.
Weight of oldest kid is 36 kg which is numerically three times more than the age of second oldest kid.
Age of second oldest kid would be 12 years. 
Since, the second oldest kid is three year younger than the oldest kid, oldest kid would be 15 years. From this we get 3y = 15, thus y = 3. So the age of youngest kid = 5 years, second youngest kid = 10 years.
Second oldest kid, whose weight is four times the age of second youngest kid
Second youngest kid = 10 years, so weight of second oldest kid = 4 × 10 = 40 kg
Weight of the youngest kid is 40% less than the second oldest kid
Weight of second oldest = 40kg, youngest kid = 40kg – 40% of 40kg = 24kg
Sum of all the weights = 129kg = 36kg + 24kg + 40kg + weight of second youngest kid
Weight of second youngest kid = 29kg

In a table form all the values are: 

1 Crore+ students have signed up on EduRev. Have you? Download the App
MCQ Test: Caselets - 3 - Question 3
Save

Directions: Study the following information carefully and answer the questions given beside.
Mr. Dexter has four kids and all were born on same date of different years. They all have birthday today. Mr. Dexter wants to buy chocolates for all his kids. But he don’t want to give each kid equal number of chocolates.
He decides to do the following thing:
He will divide the height (in centimeters) by the sum of age number with weight (in kilogram).
He arrive at this formula –
Number of chocolate = height in centimeters/(weight in kilogram + age)
The number that will come is the number of chocolates that a particular kid gets.
His second youngest kid is twice the age of the youngest kid whose age is one-third the oldest kid. The second oldest kid is three year younger than the oldest kid. Weight of oldest kid is 36 kg which is numerically three times the age of second oldest kid, whose weight is four times the age of second youngest kid. Weight of the youngest kid is 40% less than the second oldest kid. Sum of weight of all four kids is 129 kg.

Q. After 5 years from this birthday, Mr. Dexter repeat the same method of distributing the chocolates. After five years, his youngest kid has gained 25% weight while the oldest kid has weight twice the youngest kid. He distribute 6 chocolates between youngest and the oldest kid. If their heights are equal then choose the correct option.

Detailed Solution for MCQ Test: Caselets - 3 - Question 3

From common explanation, we have

After 5 years, oldest kid = 15 + 5 = 20 years, and youngest kid = 5+5 = 10 years.

Weight of youngest kid = 24kg + 25% of 24 kg = 30kg

Weight of oldest kid = 2 × weight of youngest kid = 2 × 30 = 60kg

Let the youngest kid gets ‘y’ chocolates, then the oldest will get (6 – y) chocolates.

Now, let their heights be ‘H’

Number of chocolates youngest kid get,

H = 40y ------(i)
Number of chocolates oldest kid get,

H = 80 (6 – y) -------(ii)
H = 40y = 80 (6 – y)
y = 2(6 – y) = 12 – 2y
y = 4
from (i)
H = 40 × 4 = 160 cm
Hence, option D is correct.

Common explanation:
It is given that the second youngest kid is twice the age of the youngest kid whose age is three times less than the oldest kid.
Let the age of youngest kid is ‘y’, then the second youngest kid would be 2y and the oldest would be 3y.
Weight of oldest kid is 36 kg which is numerically three times more than the age of second oldest kid.
Age of second oldest kid would be 12 years. 
Since, the second oldest kid is three year younger than the oldest kid, oldest kid would be 15 years. From this we get 3y = 15, thus y = 3. So the age of youngest kid = 5 years, second youngest kid = 10 years.
Second oldest kid, whose weight is four times the age of second youngest kid
Second youngest kid = 10 years, so weight of second oldest kid = 4 × 10 = 40 kg
Weight of the youngest kid is 40% less than the second oldest kid
Weight of second oldest = 40kg, youngest kid = 40kg – 40% of 40kg = 24kg
Sum of all the weights = 129kg = 36kg + 24kg + 40kg + weight of second youngest kid
Weight of second youngest kid = 29kg

In a table form all the values are: 

MCQ Test: Caselets - 3 - Question 4
Save

Directions: Study the following information carefully and answer the questions given beside.
Mr. Dexter has four kids and all were born on same date of different years. They all have birthday today. Mr. Dexter wants to buy chocolates for all his kids. But he don’t want to give each kid equal number of chocolates.
He decides to do the following thing:
He will divide the height (in centimeters) by the sum of age number with weight (in kilogram).
He arrive at this formula –
Number of chocolate = height in centimeters/(weight in kilogram + age)
The number that will come is the number of chocolates that a particular kid gets.
His second youngest kid is twice the age of the youngest kid whose age is one-third the oldest kid. The second oldest kid is three year younger than the oldest kid. Weight of oldest kid is 36 kg which is numerically three times the age of second oldest kid, whose weight is four times the age of second youngest kid. Weight of the youngest kid is 40% less than the second oldest kid. Sum of weight of all four kids is 129 kg.

Q. The oldest and second oldest kids get equal number of chocolates. Find the ratio of their heights if both of them got three chocolates. (oldest : second oldest)
Detailed Solution for MCQ Test: Caselets - 3 - Question 4

From common explanation, we have

The formula he used to distribute the chocolates is

Number of chocolate = 
For second oldest kid –

Height in cm = 52 × 3 = 156 cm
For oldest kid –

Height in cm = 51 × 3 = 153 cm
Ratio = oldest : second oldest = 153 : 156 = 51 : 52
Hence, option C is correct.

Common explanation:
It is given that the second youngest kid is twice the age of the youngest kid whose age is three times less than the oldest kid.
Let the age of youngest kid is ‘y’, then the second youngest kid would be 2y and the oldest would be 3y.
Weight of oldest kid is 36 kg which is numerically three times more than the age of second oldest kid.
Age of second oldest kid would be 12 years. 
Since, the second oldest kid is three year younger than the oldest kid, oldest kid would be 15 years. From this we get 3y = 15, thus y = 3. So the age of youngest kid = 5 years, second youngest kid = 10 years.
Second oldest kid, whose weight is four times the age of second youngest kid
Second youngest kid = 10 years, so weight of second oldest kid = 4 × 10 = 40 kg
Weight of the youngest kid is 40% less than the second oldest kid
Weight of second oldest = 40kg, youngest kid = 40kg – 40% of 40kg = 24kg
Sum of all the weights = 129kg = 36kg + 24kg + 40kg + weight of second youngest kid
Weight of second youngest kid = 29kg

In a table form all the values are: 

MCQ Test: Caselets - 3 - Question 5
Save

Directions: Study the following information carefully and answer the questions given beside.
Mr. Dexter has four kids and all were born on same date of different years. They all have birthday today. Mr. Dexter wants to buy chocolates for all his kids. But he don’t want to give each kid equal number of chocolates.
He decides to do the following thing:
He will divide the height (in centimeters) by the sum of age number with weight (in kilogram).
He arrive at this formula –
Number of chocolate = height in centimeters/(weight in kilogram + age)
The number that will come is the number of chocolates that a particular kid gets.
His second youngest kid is twice the age of the youngest kid whose age is one-third the oldest kid. The second oldest kid is three year younger than the oldest kid. Weight of oldest kid is 36 kg which is numerically three times the age of second oldest kid, whose weight is four times the age of second youngest kid. Weight of the youngest kid is 40% less than the second oldest kid. Sum of weight of all four kids is 129 kg.

Q. Mr. Dexter also buys some pens for his kids and he wants to distribute in this way. The kid with highest weight will get half of them, the kid with second highest weight will get half of what left after giving half the pen to the kid with highest weight. The third highest weight kid get half of what left after the first two round of distributions. If last kid gets 2 pens, ratio of weight to the number of pens for the oldest kid?
Detailed Solution for MCQ Test: Caselets - 3 - Question 5

From common explanation, we have
Let he bought ‘y’ pens.
Kid with highest weight (40kg) = y/2 pens
Number of pens left = y/2
Half of it will go to 36 kg kid = y/4
Number of pens left = y/4
Half of it will go to 29 kg kid = y/8
Number of pens left = y/8
The kid with 24kg weight will get whatever left,
so he also gets = y/8
Since he gets 2 pens, we must have:
y/8 = 2, or y = 16
Ratio of weight to the number of pens for the oldest kid
Weight of oldest kid = 36kg, pens he got
y/4 = 16/4 = 4
Ratio = 36 : 4 = 9 : 1
Hence, option C is correct.

Common explanation:
It is given that the second youngest kid is twice the age of the youngest kid whose age is three times less than the oldest kid.
Let the age of youngest kid is ‘y’, then the second youngest kid would be 2y and the oldest would be 3y.
Weight of oldest kid is 36 kg which is numerically three times more than the age of second oldest kid.
Age of second oldest kid would be 12 years. 
Since, the second oldest kid is three year younger than the oldest kid, oldest kid would be 15 years. From this we get 3y = 15, thus y = 3. So the age of youngest kid = 5 years, second youngest kid = 10 years.
Second oldest kid, whose weight is four times the age of second youngest kid
Second youngest kid = 10 years, so weight of second oldest kid = 4 × 10 = 40 kg
Weight of the youngest kid is 40% less than the second oldest kid
Weight of second oldest = 40kg, youngest kid = 40kg – 40% of 40kg = 24kg
Sum of all the weights = 129kg = 36kg + 24kg + 40kg + weight of second youngest kid
Weight of second youngest kid = 29kg

In a table form all the values are: 

MCQ Test: Caselets - 3 - Question 6
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is regarding the number of students appeared in three different exams A, B and C in four different years 2015, 2016, 2017 and 2018.
In 2015:
Students appeared in exam A was twice the students appeared in exam B. Total students appeared in three exams together was 1640. Students appeared in exam B was 40 more than students appeared in exam C.
In 2016:
Students appeared in exam B was 40% more than students appeared in exam A while students appeared in exam C was 20% more than students appeared in exam B. Total students appeared in all three exams together was 2448.
In 2017:
Ratio of students appeared in exam A to exam B was 7:9. Students appeared in exam C was 25% more than students appeared in exam B. Total students appeared in all three exams together was 2180.
In 2018:
Average of students appeared in exams A and B was 560. Students appeared in exam C was 600. Ratio of students appeared in exam A to exam C was 4 : 5.

Q. What is the difference between number of students appeared in exams B and C together in 2015 and number of students appeared in exams A and B together in 2017? 
Detailed Solution for MCQ Test: Caselets - 3 - Question 6

In 2015:
Let students appeared in exam B = a
Students appeared in exam A = 2a 
Students appeared in exam C = a – 40
So a + 2a + a – 40 = 1640
4a = 1680
a = 420
Students appeared in exam B = 420
Students appeared in exam A = 840 
Students appeared in exam C = 380
In 2017:
Let students appeared in exam A and exam B be 7c and 9c respectively.
Students appeared in exam C = 125% of 9c = 11.25c
So 7c + 9c + 11.25c = 2180
27.25c = 2180
c = 80
Students appeared in exam A = 560 
Students appeared in exam B = 720
Students appeared in exam C = 900
Number of students appeared in exams B and C together in 2015 = 420 + 380 = 800
Number of students appeared in exams A and B together in 2017 = 560 + 720 = 1280
Difference = 1280 – 800 = 480
 Hence, option B is correct.

MCQ Test: Caselets - 3 - Question 7
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is regarding the number of students appeared in three different exams A, B and C in four different years 2015, 2016, 2017 and 2018.
In 2015:
Students appeared in exam A was twice the students appeared in exam B. Total students appeared in three exams together was 1640. Students appeared in exam B was 40 more than students appeared in exam C.
In 2016:
Students appeared in exam B was 40% more than students appeared in exam A while students appeared in exam C was 20% more than students appeared in exam B. Total students appeared in all three exams together was 2448.
In 2017:
Ratio of students appeared in exam A to exam B was 7:9. Students appeared in exam C was 25% more than students appeared in exam B. Total students appeared in all three exams together was 2180.
In 2018:
Average of students appeared in exams A and B was 560. Students appeared in exam C was 600. Ratio of students appeared in exam A to exam C was 4 : 5.

Q. Ratio of number of girls to boys appeared in exam A in 2015 was 5 : 7 and 35% of total students appeared in exam C in 2017 was boys. What is the sum of number of boys appeared in exam A in 2015 and in exam C in 2017?
Detailed Solution for MCQ Test: Caselets - 3 - Question 7

In 2015:
Let students appeared in exam B = a
Students appeared in exam A = 2a
Students appeared in exam C = a – 40
So a + 2a + a – 40 = 1640
4a = 1680
a = 420
Students appeared in exam B = 420
Students appeared in exam A = 840
Students appeared in exam C = 380
In 2017:
Let students appeared in exam A and exam B be 7c and 9c respectively.
Students appeared in exam C = 125% of 9c = 11.25c
So 7c + 9c + 11.25c = 2180
27.25c = 2180
c = 80
Students appeared in exam A = 560
Students appeared in exam B = 720
Students appeared in exam C = 900
Sum of boys = 840/12 × 7 + 35% of 900 = 490 + 315 = 805
Hence, option C is correct.

MCQ Test: Caselets - 3 - Question 8
Save

In 2017, 10%, 20% and 20% of students appeared in exams A, B and C cleared the respective exams while in 2018 percentage for same was 20%, 10% and 40%. How many students cleared all three exams in these two years?
Detailed Solution for MCQ Test: Caselets - 3 - Question 8

In 2017:
Let students appeared in exam A and exam B be 7c and 9c respectively.
Students appeared in exam C = 125% of 9c = 11.25c
So 7c + 9c + 11.25c = 2180
27.25c = 2180
c = 80
Students appeared in exam A = 560
Students appeared in exam B = 720
Students appeared in exam C = 900
In 2018:
Students appeared in exam A =  600/5 × 4 = 480
Students appeared in exam B = 560 × 2 – 480 = 640
Students appeared in exam C = 600
Total students appeared = 480 + 640 + 600 = 1720
Number of students cleared exam = 10% of 560 + 20% of 720 + 20% of 900 + 20% of 480 + 10% of 640 + 40% of 600 = 56 + 144 + 180 + 96 + 64 + 240 = 780

Hence, option B is correct.

MCQ Test: Caselets - 3 - Question 9
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is regarding the number of students appeared in three different exams A, B and C in four different years 2015, 2016, 2017 and 2018.
In 2015:
Students appeared in exam A was twice the students appeared in exam B. Total students appeared in three exams together was 1640. Students appeared in exam B was 40 more than students appeared in exam C.
In 2016:
Students appeared in exam B was 40% more than students appeared in exam A while students appeared in exam C was 20% more than students appeared in exam B. Total students appeared in all three exams together was 2448.
In 2017:
Ratio of students appeared in exam A to exam B was 7:9. Students appeared in exam C was 25% more than students appeared in exam B. Total students appeared in all three exams together was 2180.
In 2018:
Average of students appeared in exams A and B was 560. Students appeared in exam C was 600. Ratio of students appeared in exam A to exam C was 4 : 5.

Q. What is the ratio of number of students appeared in exams A and B in 2016 to number of students appeared in exams A and C in 2018?
Detailed Solution for MCQ Test: Caselets - 3 - Question 9

In 2016:
Let students appeared in exam A = b
Students appeared in exam B = 140% of b = 1.4b
Students appeared in exam C = 120% of 1.4b = 1.68b
So b + 1.4b + 1.68b = 2448
4.08b = 2448
b = 600
Students appeared in exam A = 600
Students appeared in exam B = 840
Students appeared in exam C = 1008
In 2018:
Students appeared in exam A = 600/5 × 4 = 480
Students appeared in exam B = 560 × 2 – 480 = 640
Students appeared in exam C = 600
Total students appeared = 480 + 640 + 600 = 1720
Number of students appeared in exams A and B in 2016 = 600 + 840 = 1440
Number of students appeared in exams A and C in 2018 = 480 + 600 = 1080
Ratio = 1440 : 1080 = 4 : 3
Hence, option A is correct.

MCQ Test: Caselets - 3 - Question 10
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is regarding the number of students appeared in three different exams A, B and C in four different years 2015, 2016, 2017 and 2018.
In 2015:
Students appeared in exam A was twice the students appeared in exam B. Total students appeared in three exams together was 1640. Students appeared in exam B was 40 more than students appeared in exam C.
In 2016:
Students appeared in exam B was 40% more than students appeared in exam A while students appeared in exam C was 20% more than students appeared in exam B. Total students appeared in all three exams together was 2448.
In 2017:
Ratio of students appeared in exam A to exam B was 7:9. Students appeared in exam C was 25% more than students appeared in exam B. Total students appeared in all three exams together was 2180.
In 2018:
Average of students appeared in exams A and B was 560. Students appeared in exam C was 600. Ratio of students appeared in exam A to exam C was 4 : 5.

Q. Find the total number of students appeared in all three exams in all four years together.
Detailed Solution for MCQ Test: Caselets - 3 - Question 10

Total students appeared in 2015 = 1640
Total students appeared in 2016 = 2448
Total students appeared in 2017 = 2180
In 2018:
Students appeared in exam A = 600/5 × 4 = 480
Students appeared in exam B = 560 × 2 – 480 = 640
Students appeared in exam C = 600
Total students appeared = 480 + 640 + 600 = 1720
Total students appeared = 1640 + 2448 + 2180 + 1720 = 7988
Hence, option D is correct.

MCQ Test: Caselets - 3 - Question 11
Save

Directions : Study the following information carefully and answer the questions given beside.
The information given below is the investment of three Venture capitalists in a partnership for the period of 1991 – 1995.
The investments made by an individual are for the same period. The investment of Bikram in 1991 is Rs. 40000 and is equal is to the investment of Chandan in 1993. The total investment in 1994 is Rs. 24000 and the ratio of investments of Arjun, Bikram and Chandan is 8 : 9 : 7 respectively. The investments of Arjun in 1991, 1992 and 1993 are Rs. 32000, Rs. 48000 and Rs. 44000 respectively. The investment of Chandan in 1991 and 1992 are same i.e. Rs. 22000. The investment of Bikram in 1993 is Rs. 6000 more than the investment by him in 1992 i.e. Rs. 30000.

Q. Find the share of profit earned by Bikram in the year 1993, if the total profit in 1993 is Rs. 15000?
Detailed Solution for MCQ Test: Caselets - 3 - Question 11


Ratio of profit = 44000 : 36000 : 40000
Ratio of profit = 44 : 36 : 40
So the profit shared by the venture capitalist would be in the ratio of 44 : 36 : 40
Share of Bikram = 36/120 × 15000 = 4500
Hence, option C is correct.

MCQ Test: Caselets - 3 - Question 12
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is the investment of three Venture capitalists in a partnership for the period of 1991 – 1995.
The investments made by an individual are for the same period. The investment of Bikram in 1991 is Rs. 40000 and is equal is to the investment of Chandan in 1993. The total investment in 1994 is Rs. 24000 and the ratio of investments of Arjun, Bikram and Chandan is 8 : 9 : 7 respectively. The investments of Arjun in 1991, 1992 and 1993 are Rs. 32000, Rs. 48000 and Rs. 44000 respectively. The investment of Chandan in 1991 and 1992 are same i.e. Rs. 22000. The investment of Bikram in 1993 is Rs. 6000 more than the investment by him in 1992 i.e. Rs. 30000.

Q. If the share of profit of Chandan in 1991 and 1992 is Rs. 7700 and Rs. 8800 respectively, find the ratio of profit of Arjun in 1991 to that in 1992?
Detailed Solution for MCQ Test: Caselets - 3 - Question 12


For the year 1991,

For the year 1992,

So, the ratio of profits of Arjun

Hence, option D is correct.

MCQ Test: Caselets - 3 - Question 13
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is the investment of three Venture capitalists in a partnership for the period of 1991 – 1995.
The investments made by an individual are for the same period. The investment of Bikram in 1991 is Rs. 40000 and is equal is to the investment of Chandan in 1993. The total investment in 1994 is Rs. 24000 and the ratio of investments of Arjun, Bikram and Chandan is 8 : 9 : 7 respectively. The investments of Arjun in 1991, 1992 and 1993 are Rs. 32000, Rs. 48000 and Rs. 44000 respectively. The investment of Chandan in 1991 and 1992 are same i.e. Rs. 22000. The investment of Bikram in 1993 is Rs. 6000 more than the investment by him in 1992 i.e. Rs. 30000.

Q. The profit earned by Bikram in 1996 is 8% of the investment made by Bikram in 1992 and the profit of Chandan in 1996 is 10% of the investment made by Chandan in 1992. Find the ratio of profit of Chandan in 1996 to that of Bikram in 1996.
Detailed Solution for MCQ Test: Caselets - 3 - Question 13


For the year 1996,
Profit of Bikram = 8/100 × 30000 = Rs. 2400
For the year 1996,
Profit of Chandan = 10/100 × 22000 = Rs. 2200
So, the ratio of profit of Chandan in 1996 to that of Bikram in 1996

Hence, option B is correct.

MCQ Test: Caselets - 3 - Question 14
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is the investment of three Venture capitalists in a partnership for the period of 1991 – 1995.
The investments made by an individual are for the same period. The investment of Bikram in 1991 is Rs. 40000 and is equal is to the investment of Chandan in 1993. The total investment in 1994 is Rs. 24000 and the ratio of investments of Arjun, Bikram and Chandan is 8 : 9 : 7 respectively. The investments of Arjun in 1991, 1992 and 1993 are Rs. 32000, Rs. 48000 and Rs. 44000 respectively. The investment of Chandan in 1991 and 1992 are same i.e. Rs. 22000. The investment of Bikram in 1993 is Rs. 6000 more than the investment by him in 1992 i.e. Rs. 30000.

Q. Suppose all the VCs invested for one more year i.e. 1995 and the total investment of Arjun and Bikram is Rs. 56000 and invested their amounts for 24 and 16 months respectively, find for how many months Chandan invested his amount of Rs. 64,000? [Given profits of Arjun, Bikram and Chandan are Rs. 12600, Rs. 11200 and Rs. 16800 respectively]
Detailed Solution for MCQ Test: Caselets - 3 - Question 14


Let A and B be the investment made by Arjun and Bikram respectively.

Therefore, investment of Arjun = 3/7 × 56000 = 24000
So, the investment made by Bikram = 32000
Let, Chandan invested for C months
So, the ratio of Arjun and Chandan’s profit

C = 12 
Hence, option E is correct.

MCQ Test: Caselets - 3 - Question 15
Save

Directions: Study the following information carefully and answer the questions given beside.
The information given below is the investment of three Venture capitalists in a partnership for the period of 1991 – 1995.
The investments made by an individual are for the same period. The investment of Bikram in 1991 is Rs. 40000 and is equal is to the investment of Chandan in 1993. The total investment in 1994 is Rs. 24000 and the ratio of investments of Arjun, Bikram and Chandan is 8 : 9 : 7 respectively. The investments of Arjun in 1991, 1992 and 1993 are Rs. 32000, Rs. 48000 and Rs. 44000 respectively. The investment of Chandan in 1991 and 1992 are same i.e. Rs. 22000. The investment of Bikram in 1993 is Rs. 6000 more than the investment by him in 1992 i.e. Rs. 30000.

Q. If the amount of profit shared by Arjun and Bikram in 1994 is Rs. 4000 and Rs. 4500 respectively and Chandan makes 3/4th of the profit in 1995 as compared to his profit in 1994. Find the amount of Profit shared by Chandan in 1995?
Detailed Solution for MCQ Test: Caselets - 3 - Question 15

For the year 1994,
Profit of Chandan =
So, amount of Profit shared by Chandan in 1995
= 3500 × 3/4 = 2625
Hence, option A is correct.

MCQ Test: Caselets - 3 - Question 16
Save

Directions: Study the following information carefully and answer the questions given beside.
Information about number of patients who were tested positive to COVID-19 tests in five different cities of India is as follows.
Delhi has 60% more patients than Jaipur, which has 400 more than Chennai. Number of patients in Calcutta was half the number of patients in Chennai. Number of patients in Mumbai was 100 less than Chennai. Total patients were 9100 as on 31 March 2019 in all the five cities together.
It was found that out of every 200 patients, 180 recovered within 14 days, 18 took 30 days to recover and 2 died.

Q. Find average number of patients in Chennai, Calcutta and Mumbai.
Detailed Solution for MCQ Test: Caselets - 3 - Question 16

From common explanation, we have
Chennai = 1600
Calcutta = 800
Mumbai = 1500
Total = 3900
Average = 1300
Hence, option C is correct.

Common explanation : 
Let the number of patients in Delhi, Jaipur, Chennai, Calcutta, Mumbai were D, J, Ch, Cal, M respectively.
Then we have
D = 1.6J = 1.6(400+Ch)
Cal = 1/2 Ch
M = Ch – 100
Therefore, we have
D + J + Ch + Cal + M = 9100
1.6 (400 + Ch) + (400 + Ch) + Ch + 1/2 Ch + Ch – 100 = 9100
940 + 5.1Ch = 9100
Ch = 1600
Thus, patients in various cities are
Delhi = 3200
Jaipur = 2000
Chennai = 1600
Calcutta = 800
Mumbai = 1500

MCQ Test: Caselets - 3 - Question 17
Save

Directions: Study the following information carefully and answer the questions given beside.
Information about number of patients who were tested positive to COVID-19 tests in five different cities of India is as follows.
Delhi has 60% more patients than Jaipur, which has 400 more than Chennai. Number of patients in Calcutta was half the number of patients in Chennai. Number of patients in Mumbai was 100 less than Chennai. Total patients were 9100 as on 31 March 2019 in all the five cities together.
It was found that out of every 200 patients, 180 recovered within 14 days, 18 took 30 days to recover and 2 died.

Q. For each 1000 tests the numbers of people who were found positive were 130. Find out how many tests were conducted that produced 9100 total positive cases?
Detailed Solution for MCQ Test: Caselets - 3 - Question 17

From common explanation, we have
For each 1000 tests we have 130 positive.
Thus for 9100 = 70 ( × 130), we should have 70 (× 1000) = 70,000 tests.
Hence, option E is correct.

Common explanation : 
Let the number of patients in Delhi, Jaipur, Chennai, Calcutta, Mumbai were D, J, Ch, Cal, M respectively.
Then we have
D = 1.6J = 1.6(400+Ch)
Cal = 1/2 Ch
M = Ch – 100
Therefore, we have
D + J + Ch + Cal + M = 9100
1.6 (400 + Ch) + (400 + Ch) + Ch + 1/2 Ch + Ch – 100 = 9100
940 + 5.1Ch = 9100
Ch = 1600
Thus, patients in various cities are
Delhi = 3200
Jaipur = 2000
Chennai = 1600
Calcutta = 800
Mumbai = 1500

MCQ Test: Caselets - 3 - Question 18
Save

Directions: Study the following information carefully and answer the questions given beside.
Information about number of patients who were tested positive to COVID-19 tests in five different cities of India is as follows.
Delhi has 60% more patients than Jaipur, which has 400 more than Chennai. Number of patients in Calcutta was half the number of patients in Chennai. Number of patients in Mumbai was 100 less than Chennai. Total patients were 9100 as on 31 March 2019 in all the five cities together.
It was found that out of every 200 patients, 180 recovered within 14 days, 18 took 30 days to recover and 2 died.

Q. How many people died in Jaipur, Mumbai and Chennai together?
Detailed Solution for MCQ Test: Caselets - 3 - Question 18

From the common explanation, we have
It is given that out of 200 patients, only 2 dies,
thus 2/200 × 100 = 1% die.
Number of patients in Jaipur, Mumbai and Chennai = 2000 + 1500 + 1600 = 5100
Number of people who will die = 1% of 5100 = 51
Hence, option B is correct.

Common explanation : 
Let the number of patients in Delhi, Jaipur, Chennai, Calcutta, Mumbai were D, J, Ch, Cal, M respectively.
Then we have
D = 1.6J = 1.6(400+Ch)
Cal = 1/2 Ch
M = Ch – 100
Therefore, we have
D + J + Ch + Cal + M = 9100
1.6 (400 + Ch) + (400 + Ch) + Ch + 1/2 Ch + Ch – 100 = 9100
940 + 5.1Ch = 9100
Ch = 1600
Thus, patients in various cities are
Delhi = 3200
Jaipur = 2000
Chennai = 1600
Calcutta = 800
Mumbai = 1500

MCQ Test: Caselets - 3 - Question 19
Save

Directions: Study the following information carefully and answer the questions given beside.
Information about number of patients who were tested positive to COVID-19 tests in five different cities of India is as follows.
Delhi has 60% more patients than Jaipur, which has 400 more than Chennai. Number of patients in Calcutta was half the number of patients in Chennai. Number of patients in Mumbai was 100 less than Chennai. Total patients were 9100 as on 31 March 2019 in all the five cities together.
It was found that out of every 200 patients, 180 recovered within 14 days, 18 took 30 days to recover and 2 died.

Q. Number of patients in Jaipur was what percent more than Calcutta?
Detailed Solution for MCQ Test: Caselets - 3 - Question 19

From common explanation, we have
Jaipur = 2000
Calcutta = 800
Percent difference = 
Hence, option B is correct.

Common explanation: 
Let the number of patients in Delhi, Jaipur, Chennai, Calcutta, Mumbai were D, J, Ch, Cal, M respectively.
Then we have
D = 1.6J = 1.6(400+Ch)
Cal = 1/2 Ch
M = Ch – 100
Therefore, we have
D + J + Ch + Cal + M = 9100
1.6 (400 + Ch) + (400 + Ch) + Ch + 1/2 Ch + Ch – 100 = 9100
940 + 5.1Ch = 9100
Ch = 1600
Thus, patients in various cities are
Delhi = 3200
Jaipur = 2000
Chennai = 1600
Calcutta = 800
Mumbai = 1500

MCQ Test: Caselets - 3 - Question 20
Save

Directions: Study the following information carefully and answer the questions given beside.
Information about number of patients who were tested positive to COVID-19 tests in five different cities of India is as follows.
Delhi has 60% more patients than Jaipur, which has 400 more than Chennai. Number of patients in Calcutta was half the number of patients in Chennai. Number of patients in Mumbai was 100 less than Chennai. Total patients were 9100 as on 31 March 2019 in all the five cities together.
It was found that out of every 200 patients, 180 recovered within 14 days, 18 took 30 days to recover and 2 died.

Q. How many patients recovered till 30 April 2020, if all the patients in Delhi, Jaipur and Calcutta are considered?
Detailed Solution for MCQ Test: Caselets - 3 - Question 20

From common explanation, we have
It is given that out of 200 patients, 180 recovered within 14 days, 18 takes 30 days to recover
Number of patients in Delhi, Jaipur and Calcutta = 3200, 2000, and 800 = 6000
From 31 March to 30 April, 180 + 18 = 198 people out of 200 will recovered,
means 198/200 x100 = 99% people will recover.
Thus, number of people who will recover from the three cities = 99% of 6000 = 5940
Hence, option D is correct.

Common explanation: 
Let the number of patients in Delhi, Jaipur, Chennai, Calcutta, Mumbai were D, J, Ch, Cal, M respectively.
Then we have
D = 1.6J = 1.6(400+Ch)
Cal = 1/2 Ch
M = Ch – 100
Therefore, we have
D + J + Ch + Cal + M = 9100
1.6 (400 + Ch) + (400 + Ch) + Ch + 1/2 Ch + Ch – 100 = 9100
940 + 5.1Ch = 9100
Ch = 1600
Thus, patients in various cities are
Delhi = 3200
Jaipur = 2000
Chennai = 1600
Calcutta = 800
Mumbai = 1500

Information about MCQ Test: Caselets - 3 Page
In this test you can find the Exam questions for MCQ Test: Caselets - 3 solved & explained in the simplest way possible. Besides giving Questions and answers for MCQ Test: Caselets - 3, EduRev gives you an ample number of Online tests for practice

Top Courses for Banking Exams

Download as PDF

Top Courses for Banking Exams

Important Questions for MCQ Test: Caselets - 3

Find all the important questions for MCQ Test: Caselets - 3 at EduRev.Get fully prepared for MCQ Test: Caselets - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the MCQ Test: Caselets - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of MCQ Test: Caselets - 3 resources.

MCQ Test: Caselets - 3

Prepare for the MCQ Test: Caselets - 3 within the Banking Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for MCQ Test: Caselets - 3

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ Test: Caselets - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup