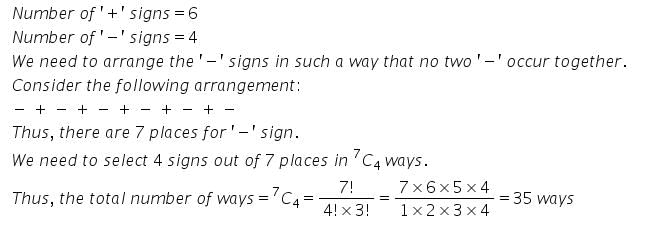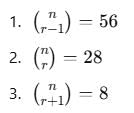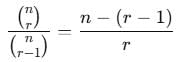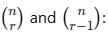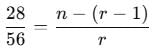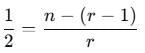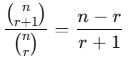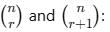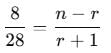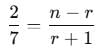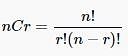Test: Permutations and Combinations- 2 - CA Foundation MCQ
30 Questions MCQ Test - Test: Permutations and Combinations- 2
The number of arrangements in which the letters of the word MONDAY be arranged so that the words thus formed begin with M and do not end with N is
The total number of ways in which six ‘+’ and four ‘–‘ signs can be arranged in a line such that no two ‘–’ signs occur together is
The number of ways in which the letters of the word MOBILE be arranged so that consonants always occupy the odd places is
5 persons are sitting in a round table in such way that Tallest Person is always on the right– side of the shortest person; the number of such arrangements is
If npr = 336 and nCr = 56, then n and r will be
If ncr–1 = 56, ncr = 28 and ncr+1 = 8, then r is equal to
A person has 8 friends. The number of ways in which he may invite one or more of them to a dinner is.
The number of ways in which a person can chose one or more of the four electrical appliances : T.V, Refrigerator, Washing Machine and a cooler is
Out of 7 gents and 4 ladies a committee of 5 is to be formed. The number of committees such that each committee includes at least one lady is
If 28C2r : 24 C2r –4 = 225 : 11, then the value of r is
There are 12 points in a plane of which 5 are collinear. The number of triangles is
The number of straight lines obtained by joining 16 points on a plane, no twice of them being on the same line is
At an election there are 5 candidates and 3 members are to be elected. A voter is entitled to vote for any number of candidates not greater than the number to be elected. The number of ways a voter choose to vote is
Every two persons shakes hands with each other in a party and the total number of hand shakes is 66. The number of guests in the party is
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
The number of ways in which 12 students can be equally divided into three groups is
The number of ways in which 15 mangoes can be equally divided among 3 students is
8 points are marked on the circumference of a circle. The number of chords obtained by joining these in pairs is
A committee of 3 ladies and 4 gents is to be formed out of 8 ladies and 7 gents. Mrs. X refuses to serve in a committee in which Mr. Y is a member. The number of such committees is
The Supreme Court has given a 6 to 3 decision upholding a lower court; the number of ways it can give a majority decision reversing the lower court is
Five bulbs of which three are defective are to be tried in two bulb points in a dark room.Number of trials the room shall be lighted is
The letters of the words CALCUTTA and AMERICA are arranged in all possible ways.The ratio of the number of there arrangements is
The ways of selecting 4 letters from the word EXAMINATION is
The number of different words that can be formed with 12 consonants and 5 vowels by taking 4 consonants and 3 vowels in each word is
Eight guests have to be seated 4 on each side of a long rectangular table.2 particular guests desire to sit on one side of the table and 3 on the other side. The number of ways in which the sitting arrangements can be made is