Test: Sets- 2 - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test - Test: Sets- 2
The following is the incomplete operation table a 4-element group.

Q.
The last row of the table is

The last row of the table is
The inclusion of which of the following sets into
S = {{1, 2}, {1, 2, 3}, {1, 3, 5}, (1, 2, 4), (1, 2, 3, 4, 5}}
is necessary and sufficient to make S a complete lattice under the partial order defined by set containment ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
How many graphs on n labeled vertices exist which have at least (n2 - 3n)/2 edges ?
Consider the set ∑* of all strings over the alphabet ∑ = {0, 1}. ∑* with the concatenation operator for strings
Let (5, ≤) be a partial order with two minimal elements a and b, and a maximum element c.
Let P : S → {True, False} be a predicate defined on S.
Suppose that P(a) = True, P(b) = False and P(x) ⇒ P(y) for all x, y ∈ S satisfying x ≤ y, where ⇒ stands for logical implication.
Q. Which of the following statements CANNOT be true ?
Let f : A → B be an injective (one-to-one) function.
Define g : 2A → 2B as :
g(C) = {f(x) | x ∈ C}, for all subsets C of A.
Define h : 2B → 2A as :
h(D) = {x | x ∈ A, f(x) ∈ D}, for all subsets D of B.
Q.
Which of the following statements is always true ?
Let ∑ = (a, b, c, d, e) be an alphabet. We define an encoding scheme as follows : g(a) = 3, g(b) = 5, g(c) = 7, g(d) = 9, g(e) = 11.
Let pi denote the i-th prime number (p1=2)
For a non-empty string s=a1…an, where each ai ∈ ∑ define 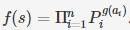
For a non-empty sequence (sj, ........ sn) of string from ∑+ defines 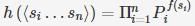
Q.
Which of the following numbers is the encoding h of a non-empty sequence of strings ?
Consider the following relations
R1(a,b) iff (a+b) is even over the set of integers
R2(a,b) iff (a+b) is odd over the set of integers
R3(a,b) iff a.b > 0 over the set of non-zero rational numbers
R4(a,b) iff |a - b| <= 2 over the set of natural numbers
Q. Which of the following statements is correct?
Consider the following statements:
S1: There exists infinite sets A, B, C such that A ∩ (B ∪ C) is finite.
S2: There exists two irrational numbers x and y such that (x+y) is rational.
Q. Which of the following is true about S1 and S2?
A relation R is defined on the set of integers as xRy if f(x + y) is even. Which of the following statements is true?
Let P(S) denotes the power set of set S. Which of the following is always true?
The binary operator ≠ is defined by the following truth table
Q. Which one of the following is true about the binary operator ≠?
Suppose L = {p, q, r, s, t} is a lattice represented by the following Hasse diagram:
For any x, y ∈ L, not necessarily distinct, x ∨ y and x ∧ y are join and meet of x, y respectively. Let L3 = {(x,y,z): x, y, z ∈ L} be the set of all ordered triplets of the elements of L. Let pr be the probability that an element (x,y,z) ∈ L3 chosen equiprobably satisfies x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z). Then
Let R be the relation on the set of positive integers such that aRb if and only if a and b are distinct and have a common divisor other than 1. Which one of the following statements about R is True?
The cardinality of the power set of {0, 1, 2 . . ., 10} is _________.
Consider two relations R1(A, B) with the tuples (1, 5), (3, 7) and R1(A, C) = (1, 7), (4, 9). Assume that R(A,B,C) is the full natural outer join of R1 and R2. Consider the following tuples of the form (A,B,C)
a = (1, 5, null),
b = (1, null, 7),
c = (3, null, 9),
d = (4, 7, null),
e = (1, 5, 7),
f = (3, 7, null),
g = (4, null, 9).
Q. Which one of the following statements is correct?
The number of onto functions (surjective functions) from set X = {1, 2, 3, 4} to set Y = {a, b, c} is ________________
Let X and Y denote the sets containing 2 and 20 distinct objects respectively and F denote the set of all possible functions defined from X and Y. Let f be randomly chosen from F. The probability of f being one-to-one is _________
Let R be a relation on the set of ordered pairs of positive integers such that ((p, q), (r, s)) ∈ R if and only if p–s = q–r. Which one of the following is true about R?
Let A be a set with n elements. Let C be a collection of distinct subsets of A such that for any two subsets S1 and S2 in C, either S1 ⊂ S2 or S2⊂ S1. What is the maximum cardinality of C?
Let R1 be a relation from A = {1, 3, 5, 7} to B = {2, 4, 6, 8} and R2 be another relation from B to C = {1, 2, 3, 4} as defined below:
- An element x in A is related to an element y in B (under R1) if x + y is divisible by 3.
- An element x in B is related to an element y in C (under R2) if x + y is even but not divisible by 3.
Q. Which is the composite relation R1R2 from A to C?
Let f be a function from a set A to a set B, g a function from B to C, and h a function from A to C, such that h(a) = g(f(a)) for all a ∈ A. Which of the following statements is always true for all such functions f and g?
A function  . defined on the set of positive integers
. defined on the set of positive integers  . satisfies the following properties :
. satisfies the following properties :
f(n)=f(n/2) if n is even
f(n)=f(n+5) if n is odd
Let 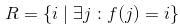 be the set of distinct values that f takes. The maximum possible size of R is ______________ .
be the set of distinct values that f takes. The maximum possible size of R is ______________ .
A binary relation R on N x N is defined as follows:
(a, b) R (c, d) if a <= c or b <= d.
Consider the following propositions:
P: R is reflexive
Q: R is transitive
Q.
Which one of the following statements is TRUE?
For the set N of natural numbers and a binary operation f : N x N → N, an element z ∊ N is called an identity for f, if f (a, z) = a = f(z, a), for all a ∊ N. Which of the following binary operations have an identity?
- f (x, y) = x + y - 3
- f (x, y) = max(x, y)
- f (x, y) = xy
Given a boolean function f (x1, x2, ..., xn), which of the following equations is NOT true
Consider the following first order logic formula in which R is a binary relation symbol. ∀x∀y (R(x, y) => R(y, x)) The formula is
Let P, Q and R be sets let Δ denote the symmetric difference operator defined as PΔQ = (P U Q) - (P ∩ Q). Using Venn diagrams, determine which of the following is/are TRUE? PΔ (Q ∩ R) = (P Δ Q) ∩ (P Δ R) P ∩ (Q ∩ R) = (P ∩ Q) Δ (P Δ R)

















