Test: Graphs- 1 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Graphs- 1
Which of the following is an advantage of adjacency list representation over adjacency matrix representation of a graph?
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
The time complexity of computing the transitive closure of a binary relation on a set of n elements is known to be:
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity.
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct? (GATE CS 2001)
How many undirected graphs (not necessarily connected) can be constructed out of a given set V= {V 1, V 2,…V n} of n vertices ?
Which of the following statements is/are TRUE for an undirected graph?
P: Number of odd degree vertices is even
Q: Sum of degrees of all vertices is eve
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is
What is the maximum number of edges in an acyclic undirected graph with n vertices?
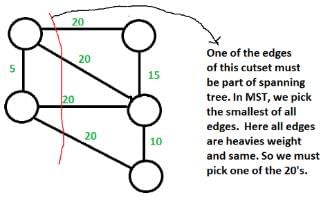
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
A sink in a directed graph is a vertex i such that there is an edge from every vertex j ≠ i to i and there is no edge from i to any other vertex. A directed graph G with n vertices is represented by its adjacency matrix A, where A[i] [j] = 1 if there is an edge directed from vertex i to j and 0 otherwise. The following algorithm determines whether there is a sink in the graph G.
i = 0
do {
j = i + 1;
while ((j < n) && E1) j++;
if (j < n) E2;
} while (j < n);
flag = 1;
for (j = 0; j < n; j++)
if ((j! = i) && E3)
flag = 0;
if (flag)
printf("Sink exists");
else
printf("Sink does not exist");
Q. Choose the correct expressions for E3
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.
- A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
- From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
- Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.
For the graph given above, possible routing tables for various nodes after they have stabilized, are shown in the following options. Identify the correct table.
Consider a simple graph with unit edge costs. Each node in the graph represents a router. Each node maintains a routing table indicating the next hop router to be used to relay a packet to its destination and the cost of the path to the destination through that router. Initially, the routing table is empty. The routing table is synchronously updated as follows. In each updation interval, three tasks are performed.
- A node determines whether its neighbours in the graph are accessible. If so, it sets the tentative cost to each accessible neighbour as 1. Otherwise, the cost is set to ∞.
- From each accessible neighbour, it gets the costs to relay to other nodes via that neighbour (as the next hop).
- Each node updates its routing table based on the information received in the previous two steps by choosing the minimum cost.
For the graph given above, possible routing tables for various nodes after they have stabilized, are shown in the following options. Identify the correct table.
Q. Continuing from the earlier problem, suppose at some time t, when the costs have stabilized, node A goes down. The cost from node F to node A at time (t + 100) is
The cyclomatic complexity of the flow graph of a program provides
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree?
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?
You are given a graph containing n vertices and m edges and given that the graph doesn’t contain cycle of odd length. Time Complexity of the best known algorithm to find out whether the graph is bipartite or not is
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.