Test: Binary Heaps - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Binary Heaps
What is the time complexity of Build Heap operation. Build Heap is used to build a max(or min) binary heap from a given array. Build Heap is used in Heap Sort as a first step for sorting.
Suppose we are sorting an array of eight integers using heapsort, and we have just finished some heapify (either maxheapify or minheapify) operations. The array now looks like this: 16 14 15 10 12 27 28 How many heapify operations have been performed on root of heap?
A max-heap is a heap where the value of each parent is greater than or equal to the values of its children. Which of the following is a max-heap? (GATE CS 2011)
A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property. Which one of the following is a valid sequence of elements in an array representing 3-ary max heap?
Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3- ary max heap found in the above question, Which one of the following is the sequence of items in the array representing the resultant heap?
Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap?
What is the content of the array after two delete operations on the correct answer to the previous question?
We have a binary heap on n elements and wish to insert n more elements (not necessarily one after another) into this heap. The total time required for this is
In a min-heap with n elements with the smallest element at the root, the 7th smallest element can be found in time.
The question was not clear in original GATE exam. For clarity, assume that there are no duplicates in Min-Heap and accessing heap elements below root is allowed.
In a binary max heap containing n numbers, the smallest element can be found in time
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is.
Given two max heaps of size n each, what is the minimum possible time complexity to make a one max-heap of size from elements of two max heaps?
A priority queue is implemented as a Max-Heap. Initially, it has 5 elements. The level-order traversal of the heap is: 10, 8, 5, 3, 2. Two new elements 1 and 7 are inserted into the heap in that order. The level-order traversal of the heap after the insertion of the elements is:
Which of the following Binary Min Heap operation has the highest time complexity?
Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stored at index i of the array (i <= n), the index of the parent is
Consider a max heap, represented by the array: 40, 30, 20, 10, 15, 16, 17, 8, 4. Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
Consider the following array of elements. 〈89, 19, 50, 17, 12, 15, 2, 5, 7, 11, 6, 9, 100〉. The minimum number of interchanges needed to convert it into a max-heap is
An operator delete(i) for a binary heap data structure is to be designed to delete the item in the i-th node. Assume that the heap is implemented in an array and i refers to the i-th index of the array. If the heap tree has depth d (number of edges on the path from the root to the farthest leaf), then what is the time complexity to re-fix the heap efficiently after the removal of the element?
A complete binary min-heap is made by including each integer in [1, 1023] exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth 0. The maximum depth at which integer 9 can appear is _____________
Which of the following sequences of array elements forms a heap?



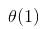 time. If Min-Heap is allowed to have duplicates, then time complexity becomes Θ(Log n). Also, if Min-Heap doesn't allow directly accessing elements below root and supports only extract-min() operation, then also time complexity becomes Θ(Log n).
time. If Min-Heap is allowed to have duplicates, then time complexity becomes Θ(Log n). Also, if Min-Heap doesn't allow directly accessing elements below root and supports only extract-min() operation, then also time complexity becomes Θ(Log n).










