Test: Hashing - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Hashing
A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.
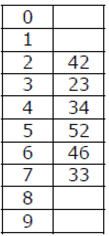
Q. Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
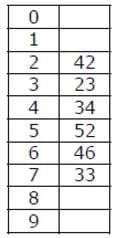
How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?

The keys 12, 18, 13, 2, 3, 23, 5 and 15 are inserted into an initially empty hash table of length 10 using open addressing with hash function h(k) = k mod 10 and linear probing. What is the resultant hash table?
Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4)mod7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that ‘_’ denotes an empty location in the table.
Given the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199) and the hash function x mod 10, which of the following statements are true?
i. 9679, 1989, 4199 hash to the same value.
ii. 1471, 6171 has to the same value.
iii. All elements hash to the same value.
iv. Each element hashes to a different value.
Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?
Which one of the following hash functions on integers will distribute keys most uniformly over 10 buckets numbered 0 to 9 for i ranging from 0 to 2020?
Given a hash table T with 25 slots that stores 2000 elements, the load factor α for T is __________
Which of the following statement(s) is TRUE?
- A hash function takes a message of arbitrary length and generates a fixed length code.
- A hash function takes a message of fixed length and generates a code of variable length.
- A hash function may give the same hash value for distinct messages.
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.



















