Test: Periodic Oscillatory & Simple Harmonic Motion (September 23) - NEET MCQ
10 Questions MCQ Test - Test: Periodic Oscillatory & Simple Harmonic Motion (September 23)
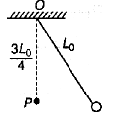
A pendulum has time period T for small oscillations. Now, an obstacle is situated below the
point of suspension O at a distance 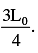 The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
point of suspension O at a distance
Three masses of 500 g, 300 g and 100 g are suspended at the end of an ideal spring as shown and are in equilibrium. When the 500 g mass is suddenly removed, the system oscillated with a period of 2 s. When 300 g mass is also removed, it will oscillate with the period


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A linear harmonic oscillator of force constant 2 x 106 Nm–1 and amplitude 0.01 m has a total mechanical energy 160 J. Among the following statements, which are correct?

A particle of mass 0.1 kg is executing SHM of amplitude 0.1 m. When the particle passes through the mean position, its KE is 8 ×10-3 J. Find the equation of motion of the particle if the initial phase of oscillation is 45˚
Two particles executing SHM with same angular frequency and amplitude A and 2A same
straight line with same position cross other in opposite direction at a distance A/3 from mean position. The phase difference between the two SHM’s is

















