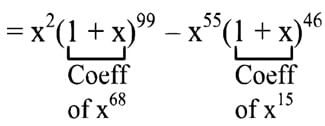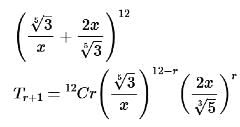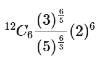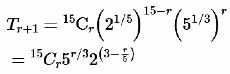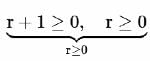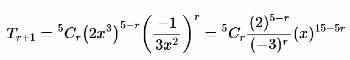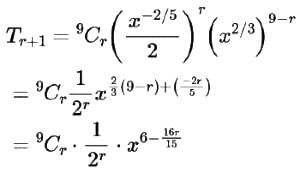Test: Binomial Theorem- 1 - JEE MCQ
25 Questions MCQ Test - Test: Binomial Theorem- 1
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
If the coefficients of x−7 and x−8 in the expansion of 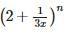 are equal then n =
are equal then n =
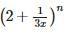 are equal then n =
are equal then n =If 2nd, 3rd and 4th terms in the expansion of (x+a)n are 240, 720 and 1080 respectively, then the value of n is
The coefficient of x70 in
x2(1 + x)98 + x3(1 + x)97 + x4(1 + x)96 + ... + x54(1 + x)46 is
99Cp - 46Cq. Then a possible value of p + q is:
If the term independent of x in the expansion of (√(ax2) + 1/2x3)10 is 105 , then a2 is equal to:
If the constant term in the expansion of( (5√3) / x + (2x) / 3√5 )12 , x ≠ 0, is α × 2⁸ × ⁵√3, then 25α is equal to:
If the coefficients of x⁴, x⁵ and x⁶ in the expansion of (1 + x)ⁿ are in the arithmetic progression, then the maximum value of n is:
The sum of all rational terms in the expansion of (21/5 + 51/3)15 is equal to:
Suppose 2 - p, p, 2 - α, α are the coefficients of four consecutive terms in the expansion of (1 + x)ⁿ.Then the value of p² - α² + 6α + 2p equals
If A denotes the sum of all the coefficients in the expansion of (1 - 3x + 10x²)ⁿ and B denotes the sum of all the coefficients in the expansion of (1 + x²)ⁿ, then:
If the second, third, and fourth terms in the expansion of (x + y)n are 135, 30, and 10/3, respectively, then 6 (n3 + x2 + y) is equal to ________.
The coefficient of x⁵ in the expansion of (2x³ - (1 / 3x²))⁵ is:
If the constant term in the expansion of (1 + 2x - 3x3)(3/2 x2 - 1/3 x)9 is p, then 108p is equal to_______.
Let the coefficient of x^r in the expansion of
(x + 3)n-1 + (x + 3)n-2(x + 2) + (x + 3)n-3(x + 2)2 + .......... + (x + 2)n-1 be αr. If
∑ (from r = 0 to n) αr = βn - γn, β, γ ∈ ℕ, then the value of β2 + γ2 equals ________."
The sum of the coefficient of x2/3 and x-2/5 in the binomial expansion of (x2/3 + (1/2)x-2/5)9 is
The sum of the coefficients of the first 50 terms in the binomial expansion of (1 - x)¹⁰⁰, is equal to
The remainder when 4282024 is divided by 21 is ________.
Number of integral terms in the expansion of (71/2 + 111/6)824 is equal to ________.