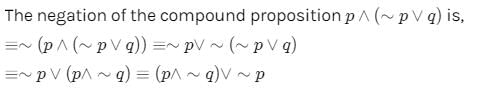Test: Mathematical Reasoning- 2 - Commerce MCQ
25 Questions MCQ Test - Test: Mathematical Reasoning- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let p and q be two propositions. Then the inverse of the implication p→q is
Let p and q be two propositions. Then the contrapositive of the implication p→q is
Let p and q be two propositions. Then the implication ∼(p↔q)∼(p↔q) is :
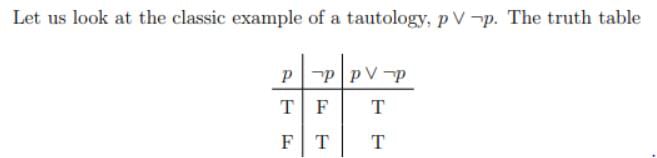
Which of the following proposition is a tautology ?
The negation of the compound statement p∨(∼p∨q) is
Which of the following is logically equivalent to ∼(∼p→q) ?
Which of the following is logically equivalent to (p∧q) ?
If p→(q∨r) is false , then the truth values of p , q and r, are respectively
Which of the following sentences is a statement ?
Let p and q be two prepositions given by p : I take only bread and butter in breakfast. q : I do not take anything in breakfast. Then , the compound proposition “ I take only bread and butter in breakfast or I do not take anything “ is represented by