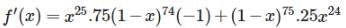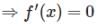Test: Application of Derivatives - 1 - JEE MCQ
26 Questions MCQ Test - Test: Application of Derivatives - 1
The instantaneous rate of change at t = 1 for the function f (t) = te−t + 9 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The equation of the tangent to the curve y = e2x at the point (0, 1) is
The smallest value of the polynomial x3−18x2+96 in the interval [0, 9] is
If the graph of a differentiable function y = f (x) meets the lines y = – 1 and y = 1, then the graph
The equation of the tangent to the curve y=(4−x2)2/3 at x = 2 is
Given that f (x) = x1/x , x>0, has the maximum value at x = e,then
Let f be a real valued function defined on (0, 1) ∪ (2, 4) such that f ‘ (x) = 0 for every x, then
The slope of the tangent to the curve x = a sin t, y = a at the point ‘t’ is
In case of strict decreasing functions, slope of tangent and hence derivative is
Let f (x) = x3−6x2+9x+18, then f (x) is strict decreasing in
Tangents to the curve y = x3 at the points (1, 1) and (– 1, – 1) are
Let f(x) = x25(1−x)75 for all x ∈ [0,1], then f (x) assumes its maximum value at
The stone projected vertically upwards moves under the action of gravity alone and its motion is described by x = 49 t – 4.9 t2 . It is at a maximum height when
Let g (x) be continuous in a neighbourhood of ‘a’ and g (a) ≠ 0. Let f be a function such that f ‘ (x) = g(x) (x−a)2 , then
Minimum value of the function f(x) = x2+x+1 is
If the line y=x is a tangent to the parabola y=ax2+bx+c at the point (1,1) and the curve passes through (−1,0), then
At which point the line x/a + y/b = 1, touches the curve y = be-x/a


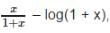 where x>0, then f is
where x>0, then f is