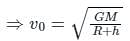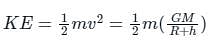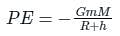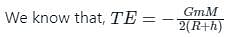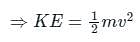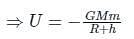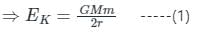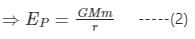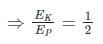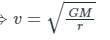NEET Exam > NEET Tests > Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - NEET MCQ
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - NEET MCQ
Test Description
10 Questions MCQ Test - Test: Earth Satellites and Energy of an Orbiting Satellite (August 12)
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) for NEET 2024 is part of NEET preparation. The Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) questions and answers have been prepared
according to the NEET exam syllabus.The Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) MCQs are made for NEET 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) below.
Solutions of Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) questions in English are available as part of our course for NEET & Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) solutions in
Hindi for NEET course.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free. Attempt Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) | 10 questions in 20 minutes | Mock test for NEET preparation | Free important questions MCQ to study for NEET Exam | Download free PDF with solutions
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 1
The total energy of a circularly orbiting satellite is-
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 1
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 2
Satellites orbiting the earth have finite life and sometimes debris of satellites fall to the earth. This is because,
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 3
The ratio of kinetic energy and the potential energy of the satellite rotating around the earth is:
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 3
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 4
The relationship between total energy (E) of an orbiting satellite and its kinetic energy (KE) is given by-
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 4
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 5
A ball is dropped from a satellite revolving around the earth at a height of 120 km. The ball will
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 5
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 6
A satellite is orbiting the Earth in a circular orbit of radius R. Choose the correct statement from the following.
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 6
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 7
The escape velocity from the surface of the Earth is approximately:
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 7
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 8
Which of the following quantities remains constant for a satellite in a circular orbit around the Earth?
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 8
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 9
If a satellite is in a geostationary orbit, its orbital period is:
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 9
Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 10
The total energy of a satellite cannot be zero because:
Detailed Solution for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) - Question 10
Information about Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) Page
In this test you can find the Exam questions for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12) solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Earth Satellites and Energy of an Orbiting Satellite (August 12), EduRev gives you an ample number of Online tests for practice
Download as PDF