RD Sharma Test: Real Numbers - 1 - Class 10 MCQ
25 Questions MCQ Test - RD Sharma Test: Real Numbers - 1
A number when divided by 61 gives 27 as quotient and 32 as remainder .Find the number
If two positive integers ‘a’ and ‘b’ are written as a = pq2 and b = p3q, where ‘p’ and ‘q’ are prime numbers, then LCM(a, b) =
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The HCF and LCM of two numbers is 9 and 459 respectively. If one of the number is 27, then the other number is
If a is a non-zero rational and √b is irrational, then a√b is:
Every positive even integer is of the form ____ for some integer ‘q’.
If HCF(a, b) = 12 and a × b = 1800, then LCM(a, b) is
If d is the HCF of 56 and 72, then values of x,y satisfying d = 56 x+72y :
The largest number which divides 70 and 125, leaving remainders 5 and 8 respectively, is
Every positive odd integer is of the form ________ where ‘q’ is some integer.
The HCF of the smallest prime number and the smallest composite number is
The decimal expansion of 987/10500 will terminate after
For any two positive integers a and b, there exist (unique) whole numbers q and r such that
The least positive integer divisible by 20 and 24 is
The largest number which divides 245 and 1029 leaving remainder 5 in each case is
What is the number x? The LCM of x and 18 is 36. The HCF of x and 18 is 2.
If ‘a’ and ‘b’ are both positive rational numbers, then
The decimal expansion of 21/24 will terminate after
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is


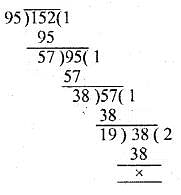
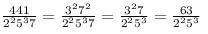
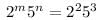 with m = 2 , n = 3.
with m = 2 , n = 3.