Test: Equations Reducible to Quadratic Form - Grade 9 MCQ

Ruhi’s mother is 26 years older than her
So let Ruhi’s age is x
So mother’s age is x+26
The product of their ages 3 years from now will be 360
So After three years , Ruhi’s age will be x+3
Mother’s age will be x+26+3=x+29
Product of their ages =(x + 3)(x + 29)=360
x²+(3+29)x+87=360
x²+32x-273=0

Let x and (16 - x) are two parts of 16 where (16 - x) is longer and x is smaller .
A/C to question,
2 × square of longer = square of smaller + 164
⇒ 2 × (16 - x)² = x² + 164
⇒ 2 × (256 + x² - 32x ) = x² + 164
⇒ 512 + 2x² - 64x = x² + 164
⇒ x² - 64x + 512 - 164 = 0
⇒ x² - 64x + 348 = 0
⇒x² - 58x - 6x + 348 = 0
⇒ x(x - 58) - 6(x - 58) = 0
⇒(x - 6)(x - 58) = 0
⇒ x = 6 and 58

But x ≠ 58 because x < 16
so, x = 6 and 16 - x = 10

Hence, answer is 6 and 10.

Roots of the equation means a value of x such that the equation becomes zero when that value is substituted. If the equation can be represented into product of two linear equations then the roots can be found by keeping each of the equation equal to zero.We know two numbers in multiplication is equal to zero only when either of the number is zero.So we get zeros of the equation putting the two linear equations equal to 0

Let us say that the sides of the two squares are 'a' and 'b'
Sum of their areas = a² + b² = 468
Difference of their perimeters = 4a - 4b = 24
=> a - b = 6
=> a = b + 6
So, we get the equation
(b + 6)² + b² = 468
=> 2b² + 12b + 36 = 468
=> b² + 6b - 216 = 0
=> b = 12
=> a = 18
The sides of the two squares are 12 and 18.

Formula for finding the roots of a quadratic equation is

So since 
b² - 4ac = 0, putting this value in the equation

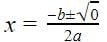
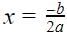So there are repeated roots