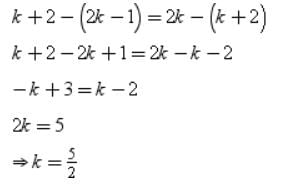Test: Introduction to Arithmetic Progression - Class 10 MCQ
20 Questions MCQ Test - Test: Introduction to Arithmetic Progression
Roots of quadratic equation x2 – 3x = 0, will be
For an A.P. the third and the fifth terms are given as 10 and 16 .What is the fourth term and the common difference?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If p, q, r, s, t are the terms of an A.P. with common difference -1 the relation between p and t is:
The weights of 11 students selected for a team are noted in ascending order and are in A. P. The lowest value is 45 Kg, and the middle value is 55 Kg. What is the difference between the two values placed consecutively ?
Is the sequence, whose general term is 5n2 + 2n + 3 an AP?
Find the next two terms of the A.P.:- -10, -6,-2…
If a + 1, 2a + 1, 4a – 1 are in A.P., then value of ‘a’ is:
Give that an A.P. has term as 5 and common differences as 2. What is the A.p.?
The 5th term of an A.P. is 18, the common difference is 2. What is the first term ?
Ramesh’s salary in February 2008 is Rs. 10,000. If he’s promised an increase of Rs. 1000 every year, what would be his salary in Feb 2011?
Given an A.P. few of whose terms are x, y, 2, 4, 6, 8,………. What must be the values of x and y?
If p – 1, p + 3, 3p – 1 are in A.P., then p is equal to:
Which of the following is an A.P with -10 as first term and 2 as the common difference?
Amit starts his exercise regime with 25 push ups on Monday. He plans to increase 5 push ups every following Monday. How many push ups will he be doing on the 3rd Monday since he started?
For what values of k can the following numbers form an A.P:2k-1,k+2,2k
From an A.P. 5 consecutive terms are required to be written. The central term out of the five terms is given as 5 and it’s informed that the common difference of the A.P. is 4. Write the 5 terms in the correct sequence.
If 4/5, a, 2 are three consecutive terms of an A.P., then the value of a is:
If a - b, 0 and a + b are consecutive terms of an AP then
The angles of a triangle in A.P. the smallest being half of the greatest. So what are the angles ?