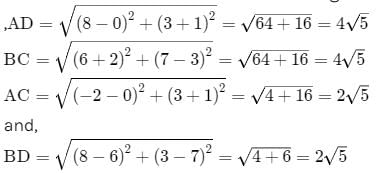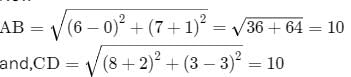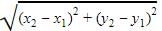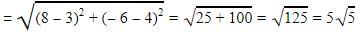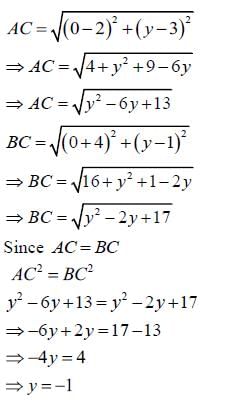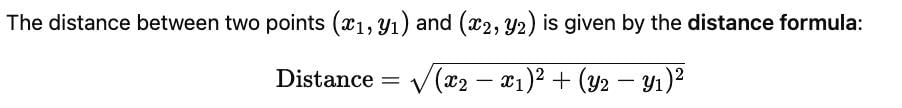Test: Distance Formula - Grade 10 MCQ
20 Questions MCQ Test - Test: Distance Formula
The coordinates of the centre of a circle passing through (1, 2), (3, – 4) and (5, – 6) is:
One end of a line of length 10 units is at the point (-3, 2). If the ordinate of the other end be 10, then the abscissa will be
The horizontal and vertical lines drawn to determine the position of a point in a Cartesian plane are called
Let P(x, y) be equidistant from the points A (7, 1) and (3, 5).Find a relation between x and y.
If the four points (0,-1), (6,7),(-2,3) and (8,3) are the vertices of a rectangle, then its area is
The perimeter of a triangle with vertices (0, 4) (0, 0) and (3, 0) is:
The ordinate of a point is twice its abscissa. If its distance from the point (4,3) is √10, then the coordinates of the point are
The perimeter of the triangle formed by the points A(0,0), B(1,0) and C(0,1) is
The value of k, if the point P(0,2) is equidistant from A(3,k) and B(k,5) is
If A and B are the points (-6, 7) and (-1, -5) respectively, then the distance 2AB is equal to
The values of x and y, if the distance of the point (x,y) from (-3,0) as well as from (3,0) is 4 are
The point on y-axis that is equidistant from (2,3) and (-4,1) is
The point on x-axis which is equidistant from (5,9) and (-4,6) is
The distance of the point P(6,-6) from the origin is equal to
The distance between the points P (-6,7) and Q (-1,-5) is
The condition that the point (x,y) may lie on the line joining (3,4) and (-5,-6) is
The points (3, 2), (0, 5), (-3, 2) and (0, -1) are the vertices of a quadrilateral. Which quadrilateral is it?