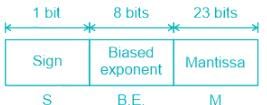
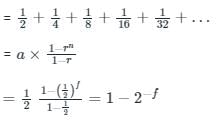Test: Floating Point Number Representation - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Floating Point Number Representation
Consider three floating-point numbers A, B and C stored in registers RA, RB and RC, respectively as per IEEE-754 single-precision floating point format. The 32-bit content stored in these registers (in hexadecimal form) are as follows.
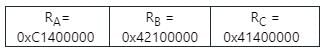
Which one of the following is FALSE?
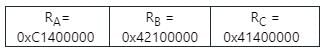
Which one of the following is FALSE?
A floating-point (FP) number is said to be normalized, if the most significant bit of the mantissa is
If we decide to stay away from IEEE 754 format by making our Exponent field 10 bits wide and our Mantissa field 21 bits wide, then which of the following statement is TRUE?
Let R1 and R2 be two 4-bit registers that store numbers in 2’s complement form. For the operation R1 + R2, which one of the following values of R1 and R2 gives an arithmetic overflow?
Given the following binary number in 32-bit (single precision) IEEE-754 format:
00111110011011010000000000000000
The decimal value closest to this floating-point number is
What is the range of the exponent E in IEEE 754 Double Precision (Binary64) format?
Consider three registers R1, R2 and R3 that store numbers in IEEE-754 single precision floating point format. Assume that R1 and R2 contain the values (in hexadecimal notation) 0x42200000 and 0xC1200000, respectively.
If R3 = R1/R2, what is the value stored in R3?
In IEEE floating point representation, the hexadecimal number 0xC0000000 corresponds to
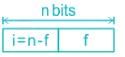
The n-bit fixed-point representation of an unsigned real number X uses f bits for the fraction part. Let i = n - f. The range of decimal values for X in this representation is.
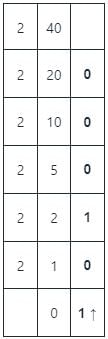
The decimal floating-point number -40.1 represented using IEEE-754 32-bit representation and written in hexadecimal form is _____