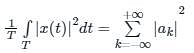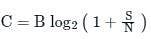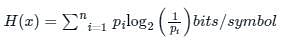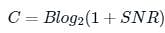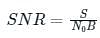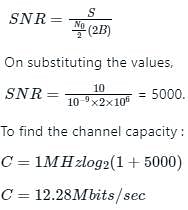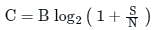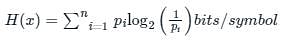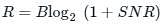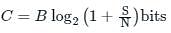Test: Channel Capacity - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Channel Capacity
Match List I with List II:
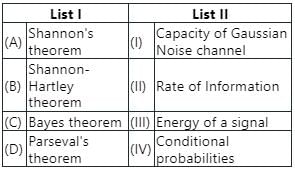
Choose the correct answer from the options given below:

Choose the correct answer from the options given below:
The information capacity (bits/sec) of a channel with bandwidth C and transmission time T is given by
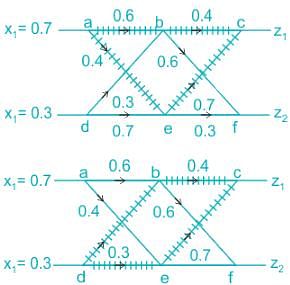
Two binary channels have been connected in a cascade as shown in the figure.
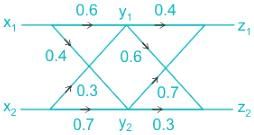
It is given that P(x1) = 0.7 and P(x2) = 0.3, then choose correct option from below.

It is given that P(x1) = 0.7 and P(x2) = 0.3, then choose correct option from below.
The maximum rate at which nearly error-free data can be theoretically transmitted over a communication channel is defined as
The Shannon limit for information capacity I is
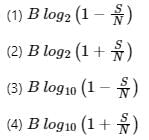
Where:
N = Noise power (W)
B = Bandwidth (Hz)
S = Signal power (W)
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9) W/Hz?
In the communication system, if for a given rate of information transmission requires channel bandwidth, B1 and signal-to-noise ratio SNR1. If the channel bandwidth is doubled for same rate of information then a new signal-to-noise ratio will be
An Ideal power limited communication channel with additive white Gaussian noise is having 4 kHz band width and Signal to Noise ratio of 255. The channel capacity is: