Test: Perpendicular From Centre To Chord - Grade 9 MCQ
10 Questions MCQ Test - Test: Perpendicular From Centre To Chord
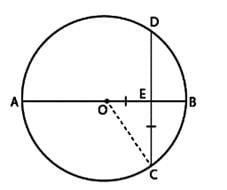
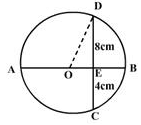
A circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, the radius of the circle is
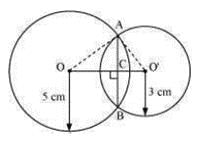
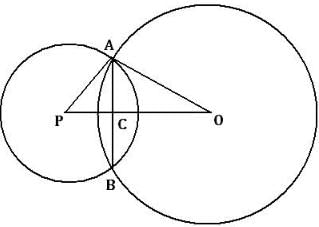
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. The length of the common chord is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The length of chord which is at a distance of 12 cm from centre of circle of radius 13 cm is:
AD is a diameter of a circle and AB is chord. If AB = 24 cm, AD = 30 cm, the distance of AB from the centre of the circle is :
The perpendicular distance of a chord 8 cm long from the centre of a circle of radius 5 cm is
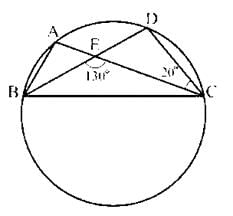
A, B, C and D are four points on a circle. AC and BD intersect at E such that angle BEC = 140° and angle ECD = 25°, then angle BAC is
The radius of a circle which has a 6 cm long chord, 4 cm away from the centre of the circle is
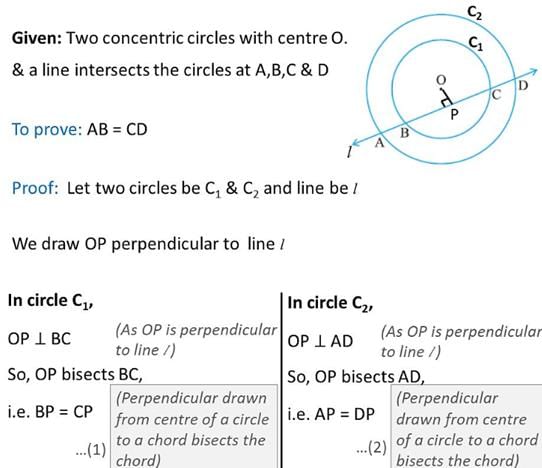
Two concentric circles are intersected by a line L at A, B, C and D. Then
In the figure, AD is a straight line. OP is perpendicular to AD and O is the centre of both the circles. If AO = 34 cm, OB = 20 cm and OP = 16 cm, then the length of AD is
Two circles of radii10 cm and 8 cm intersect and the length of the common chord is 12 cm. The distance between their centers is
Top Courses for Grade 9
Important Questions for Perpendicular From Centre To Chord
Perpendicular From Centre To Chord MCQs with Answers
Online Tests for Perpendicular From Centre To Chord
|
© EduRev
|
Education Revolution
|
Follow Us
|
