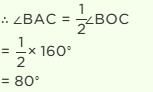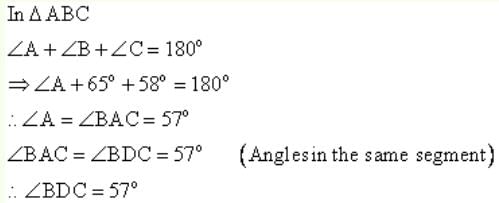All Courses
Get the App Signup / Login
Sign in Open App
Grade 9 Exam  >  Grade 9 Tests  >  Test: Properties of Equal Chords - Grade 9 MCQ

Test: Properties of Equal Chords - Grade 9 MCQ


Test Description

10 Questions MCQ Test - Test: Properties of Equal Chords

Test: Properties of Equal Chords for Grade 9 2024 is part of Grade 9 preparation. The Test: Properties of Equal Chords questions and answers have been prepared according to the Grade 9 exam syllabus.The Test: Properties of Equal Chords MCQs are made for Grade 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Properties of Equal Chords below.
Solutions of Test: Properties of Equal Chords questions in English are available as part of our course for Grade 9 & Test: Properties of Equal Chords solutions in Hindi for Grade 9 course. Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free. Attempt Test: Properties of Equal Chords | 10 questions in 10 minutes | Mock test for Grade 9 preparation | Free important questions MCQ to study for Grade 9 Exam | Download free PDF with solutions
Test: Properties of Equal Chords - Question 1
Save

XY and PQ are two parallel chords of a circle on opposite side of the centre O and radius of circle is 13 cm. if PQ = 10 cm and XY = 24 cm, find the distance between PQ and XY.

Test: Properties of Equal Chords - Question 2
Save

In the given figure, the measure of angle BCD is

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Properties of Equal Chords - Question 3
Save

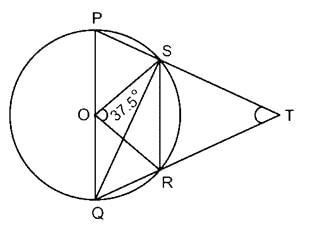
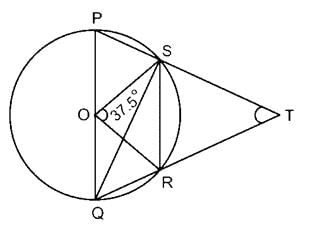
In the given figure ∠SOR = 37.5° find the value of ∠PTQ.

Detailed Solution for Test: Properties of Equal Chords - Question 3

∠SOR = 37.5° 

∠SQT = 1/2 ∠SOR (Angle at the circumference is half of the angle at the centre)

⇒ 37.5°/2

⇒ 18.75°                                                                                             

∠QSP = 90° (angle made from the diameter to the circumference is 90°)

Now,

∠PSQ + ∠QST = 180° (Linear pair angle)

∠QST = 180° - 90° = 90°

In ∆QST,

∠STQ = 180° - (90° + 18.75°)

⇒ ∠STQ = 71.25°

Test: Properties of Equal Chords - Question 4
Save

Chords of a circle, equidistant from the centre are
Test: Properties of Equal Chords - Question 5
Save

In the figure, O is the centre of the circle and the measure of arc ABC is 100o. The measure of angle ABC will be
Test: Properties of Equal Chords - Question 6
Save

A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90° and 110° respectively. Then the measure of angle BAC is
Detailed Solution for Test: Properties of Equal Chords - Question 6

Given: ∠BOA=90∘ and ∠AOC=110∘

We know that angles around a point add up to 360∘

∴∠BOC+∠BOA+∠AOC=360∘

⇒∠BOC+90∘+110∘=360∘

⇒∠BOC=360∘−200∘

∠BOC=160∘

We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

Arc BC is subtending ∠BOC at the center and ∠BAC on the remaining part of the circle, so ∠BOC=2×∠BAC

Test: Properties of Equal Chords - Question 7
Save

The angle which, an arc of a circle subtends at the centre is ….. the angle which it subtends at any point on the remaining part of the circumference.
Detailed Solution for Test: Properties of Equal Chords - Question 7
Given : An arc ABC of a circle with center O , and a point C on the remaining part of the circumference.
To Prove : Angle AOB =  Twice angle ABC
Construction : Join OC and produce it to a suitable point D
Proof : Let angles 1,2,3,4,5,6 be as shown in figure 
              a) OA=OB=OC [RADII OF THE SAME CIRCLE ARE EQUAL]
              b)1=4,2=3 [ANGLES OPPOSITE TO EQUAL SIDES ARE EQUAL]
              c)5=4+1=Twice angle1 [EXTERIOR ANGLE PROPERTY] 
              d)6=2+3=Twice angle 2 [EXTERIOR ANGLE PROPERTY]
              e)5+6=Twice angle (1+2) [ADD STATEMENT c AND d]
              f)Angle AOB = Twice angle ACB [WHOLE = SUM OF ALL ITS PARTS]

Test: Properties of Equal Chords - Question 8
Save

In the figure, angle ABC = 65° and angle ACB = 58°, the measure of angle BDC is
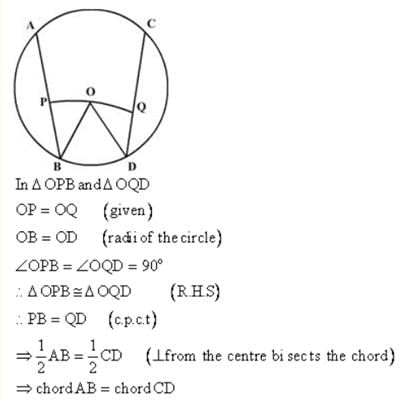
Test: Properties of Equal Chords - Question 9
Save

Two equal chords AB and CD of a circle are such that the length of perpendicular OE on CD = 5 cm. If OF is the perpendicular on AB, then OF =​
Test: Properties of Equal Chords - Question 10
Save

In the given figure, angle OAC is 35°, angle ADC is
Information about Test: Properties of Equal Chords Page
In this test you can find the Exam questions for Test: Properties of Equal Chords solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Properties of Equal Chords, EduRev gives you an ample number of Online tests for practice

Top Courses for Grade 9

Download as PDF

Top Courses for Grade 9

Important Questions for Properties of Equal Chords

Find all the important questions for Properties of Equal Chords at EduRev.Get fully prepared for Properties of Equal Chords with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Properties of Equal Chords syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Properties of Equal Chords resources.

Properties of Equal Chords MCQs with Answers

Prepare for the Properties of Equal Chords within the Grade 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Properties of Equal Chords

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Properties of Equal Chords with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup