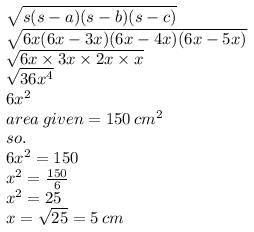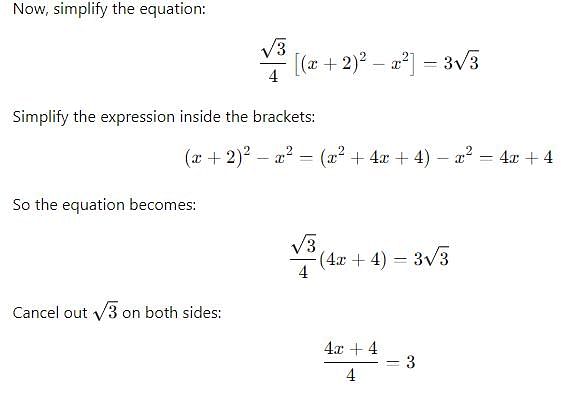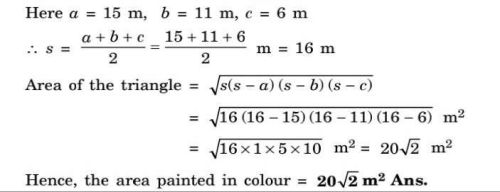Test: Introduction To Heron's Formula - Class 9 MCQ
20 Questions MCQ Test - Test: Introduction To Heron's Formula
The area of a triangle is 150 cm2 and its sides are in the ratio 3 : 4 : 5. What is its perimeter?
The area of triangle, whose sides are 15 cm, 25 cm and 14 cm:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The area of an equilateral triangle of side 6 cm is
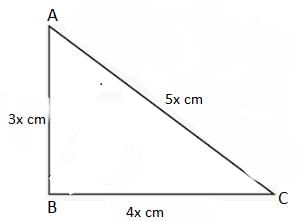
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
If each side of an equilateral triangle is increased by 2 cm, then its area increases by 3√3 cm2. The length of its each side and its area are respectively equal to
The area of quadrilateral PQRS, in which PQ = 7 cm, QR = 6 cm, RS = 12 cm, PS = 15 cm and PR = 9 cm:
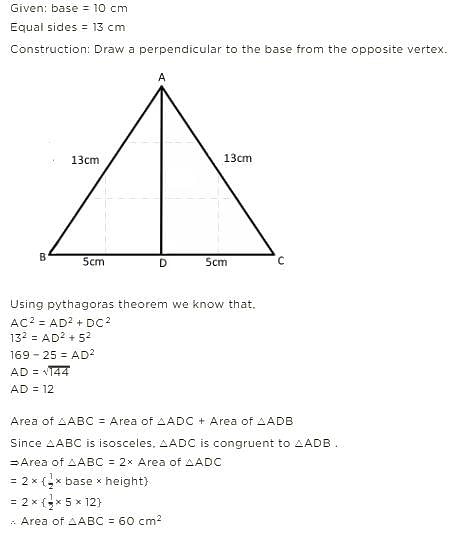
The base of an isosceles triangle is 10 cm and one of its equal sides is 13 cm. The area of the triangle is
The lengths of a triangle are 6 cm, 8 cm and 10 cm. Then the length of perpendicular from the opposite vertex to the side whose length is 8cm is:
The perimeter of an isosceles right angled triangle having an area of 200 cm2 is
A carpenter had to make a triangle with sides 5, 6, 5 units. By mistake he made one with sides 5, 8, 5 units. The difference between their areas is:
The area of a right triangle of height 15 m and base 20 m is
The sides of a triangle are in the ratio of 5: 12: 13. If its perimeter is 60 cm, then what is its area?
The area of an equilateral triangle of side 14 cm is
The sides of a triangle are in the ratio 25 : 17 : 12 and its perimeter is 540m. The area of the triangle is
The area of an equilateral triangle with perimeter 18x is:
The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Its area is
The area of a right triangle with base 5 m and altitude 12 m is
There is a slide in a park. One of its side walls has been painted in some colour with a message “Keep the park green and Clean”. If sides of the wall are 15m, 11 m and 6 m, the area painted in colour is________.
The area of a triangle whose sides are 13 cm, 14 cm and 15 cm is
The area of a triangle with given two sides 18 cm and 10 cm, respectively and a perimeter equal to 42 cm is: