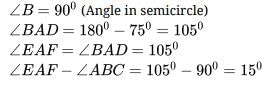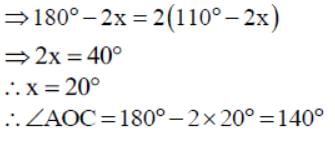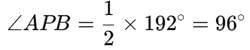Get the App Signup / Login

Grade 9 Exam > Grade 9 Tests > Test: Circles- 2 - Grade 9 MCQ

Test: Circles- 2 - Grade 9 MCQ

Test Description

25 Questions MCQ Test - Test: Circles- 2

Test: Circles- 2 for Grade 9 2024 is part of Grade 9 preparation. The Test: Circles- 2 questions and answers have been prepared according to the Grade 9 exam syllabus.The Test: Circles- 2 MCQs are made for Grade 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Circles- 2 below.

Solutions of Test: Circles- 2 questions in English are available as part of our course for Grade 9 & Test: Circles- 2 solutions in Hindi for Grade 9 course. Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free. Attempt Test: Circles- 2 | 25 questions in 25 minutes | Mock test for Grade 9 preparation | Free important questions MCQ to study for Grade 9 Exam | Download free PDF with solutions

Test: Circles- 2 - Question 1

Save

AB is a chord of a circle with radius ‘r’. If P is any point on the circle such that ∠APB is a right angle , then AB is equal to

A.
3r
B.
r
C.
2r
D.
r²

Test: Circles- 2 - Question 2

Save

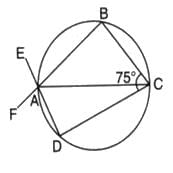
In the given figure, AC is a diameter of the given circle and ∠BCD = 75^o. Then, ∠EAF−∠ABC is equal to

A.
15^o
B.
25^o
C.
20^o
D.
10^o

Detailed Solution for Test: Circles- 2 - Question 2

1 Crore+ students have signed up on EduRev. Have you? Download the App

Test: Circles- 2 - Question 3

Save

The region between chord and either of the arc is called

A.
a sector
B.
a semicircle
C.
a segment
D.
a quarter circle

Test: Circles- 2 - Question 4

Save

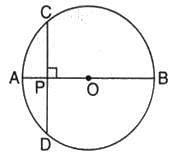
P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is

A.
16 cm
B.
20 cm
C.
10 cm
D.
8 cm

Detailed Solution for Test: Circles- 2 - Question 4

AP+PB=AB [diameter of circle]
4+16=20[diameter]
so r=AO = CO=10
so clearly PO= OA-AP=10-4=6
PO=6 OC=10 So just apply pythagoreus theorem in triangle PCO
so CP will come 8 So chord CD = 2x8 = 16

Test: Circles- 2 - Question 5

Save

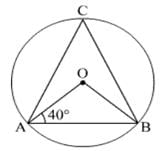
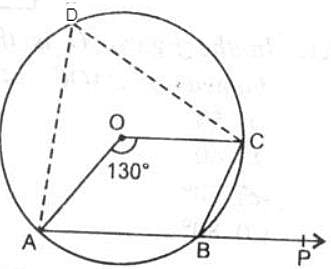
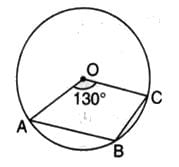
Arc ABC subtends an angle of 130^o at the centre O of the circle. AB is extended to P. Then ∠CBP equals :

A.
60^o
B.
70^o
C.
130^o
D.
65^o

Detailed Solution for Test: Circles- 2 - Question 5

Test: Circles- 2 - Question 6

Save

Chords AB and CD intersect at right angles. If ∠BAC = 40^o, then ∠ABD is equal to

A.
45^o
B.
50^o
C.
60^o
D.
none of these

Test: Circles- 2 - Question 7

Save

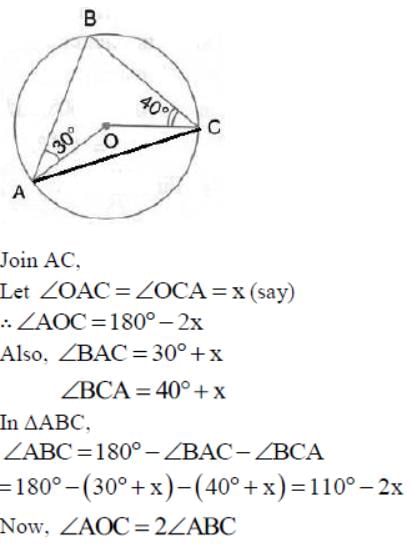
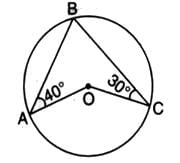
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40^o and 30^o respectively. Then, the measure of ∠AOC is

A.
170^o
B.
120^o
C.
110^o
D.
140^o

Detailed Solution for Test: Circles- 2 - Question 7

(Angle at the centre is double the angle at the circumference subtended by the same chord)

Test: Circles- 2 - Question 8

Save

In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to

A.
72^o
B.
98^o
C.
90^o
D.
96^o

Test: Circles- 2 - Question 9

Save

In the given figure, if ∠AOB = 80^o and ∠ABC = 30^o , then ∠CAO is equal to

A.
30^o
B.
60^o
C.
80^o
D.
40^o

Detailed Solution for Test: Circles- 2 - Question 9

2ACB=AOB
ACB=40
CAB+ACB+ABC=180
CAB=180-70
CAB=110
since,OA=OB(radius)
OAB=OBA

AOB+OAB+OBA=180
2OBA=100
OBA=50

CAO=CAB-OBA=110-5O
CAO=60^o

Test: Circles- 2 - Question 10

Save

In the figure, O is the centre of eh circle and ∠AOB = 80^o. The value of x is :

A.
40^o
B.
160^o
C.
60^o
D.
30^o

Detailed Solution for Test: Circles- 2 - Question 10

the angle subtend at center is double of the angle at the arc

so: 2x=80

so x=40

Test: Circles- 2 - Question 11

Save

In the given figure if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to

A.
4 cm
B.
3 cm
C.
5 cm
D.
2 cm

Test: Circles- 2 - Question 12

Save

If ∠OAB = 40^o, then the measure of ∠ACB is

A.
20^o
B.
50^o
C.
80^o
D.
40^o

Test: Circles- 2 - Question 13

Save

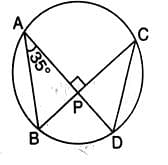
Chords AD and BC intersect each other at right angles at point P. ∠DAB = 35^o, then ∠ADC is equal to

A.
55^o
B.
45^o
C.
35^o
D.
65^o

Test: Circles- 2 - Question 14

Save

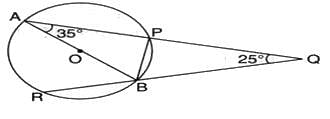
In the given figure, AB is a diameter of the circle APBR. APQ and RBQ are straight lines. If ∠A = 35^o and , then the measure of ∠PBR is

A.
165^o
B.
115^o
C.
155^o
D.
135^o

Test: Circles- 2 - Question 15

Save

In the figure, O is the center of the circle. If ∠OAB = 40^o, then ∠ACB is equal to :

A.
60^o
B.
70^o
C.
50^o
D.
40^o

Test: Circles- 2 - Question 16

Save

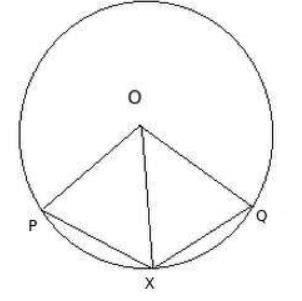
X is a point on a circle with centre O. If X is equidistant from the two radii OP, OQ, then arc PX : arc PQ is equal to

A.
it is 1 : 2
B.
it is 1 : 1
C.
it is 2 : 1
D.
it is 2 : 3

Detailed Solution for Test: Circles- 2 - Question 16

Test: Circles- 2 - Question 17

Save

BC is a diameter of the circle and ∠BAO = 60^o . Then ∠ADC is equal to

A.
45^o
B.
30^o
C.
60^o
D.
90^o

Test: Circles- 2 - Question 18

Save

What fraction of the whole circle is minor arc RP in the given figure ?

A.
1/5 of the circle
B.
1/2 of the circle
C.
1/4 of the circle
D.
1/3 of the circle

Test: Circles- 2 - Question 19

Save

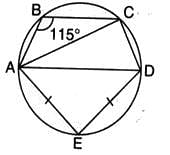
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115^o, then the measure of ∠CAE is

A.
70^o
B.
90^o
C.
80^o
D.
60^o

Test: Circles- 2 - Question 20

Save

In the figure, if ∠DAB = 60^o, ∠ABD = 50^o, then ∠ACB is equal to :

A.
60^o
B.
50^o
C.
70^o
D.
80^o

Test: Circles- 2 - Question 21

Save

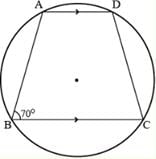
If ABCD is a cyclic trapezium in which AD ║ BC and ∠B = 60^o, then ∠BCD is equal to

A.
60^o
B.
80^o
C.
100^o
D.
None of the above

Test: Circles- 2 - Question 22

Save

In the given figure, O is the centre of the circle and ∠AOC = 130^o. Then ∠ABC is equal to

A.
115^o
B.
130^o
C.
65^o
D.
165^o

Detailed Solution for Test: Circles- 2 - Question 22

360^o - 130^o =230^o

Therefore, angle ABC =1/2reflex angle AOC

Angle ABC =1/2 230^o

So, angle ABC =115^o

Test: Circles- 2 - Question 23

Save

In the given circle, O is the centre and ∠BDC = 42^o. Then, ∠ACB is equal to

A.
58^o
B.
42^o
C.
52^o
D.
48^o

Detailed Solution for Test: Circles- 2 - Question 23

In ∆ BDC and ∆ BAC
Angle BAC = BDC
(angle made on same segment BC)
Since ABC is making right angle (90)
So,
In ∆ABC
ABC +BAC+ACB=180
(angle sum property of triangle)
90+42+ACB=180
ACB=180-132
ACB=48^o

Test: Circles- 2 - Question 24

Save

AOB is the diameter of the circle. If ∠AOE = 150^o, then the measure of ∠CBE is

A.
120^o
B.
125^o
C.
105^o
D.
115^o

Test: Circles- 2 - Question 25

Save

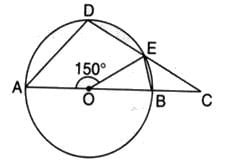
In the given figure, a circle is centred at O. The value of x is :

A.
55^o
B.
70^o
C.
110^o
D.
125^o

Information about Test: Circles- 2 Page

In this test you can find the Exam questions for Test: Circles- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Circles- 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Grade 9

Download as PDF

Top Courses for Grade 9

Join with a free account

Get Instant Access to 1000+ FREE Docs, Videos & Tests

10,000,000

Users

100+

Exams

3,25,000

Docs and Videos

75,000

Tests

I have an EduRev Account • Sign Up with Email

Attempt this test on App!

Get detailed analysis along with solutions of each question.

Open in App

Not Now

Schools

Medical
Non- Medical
Commerce
Humanities
CBSE Class 10
CBSE Class 9
CBSE Class 8
CBSE Class 7
CBSE Class 6
CBSE Class 5
CBSE Class 4
CBSE Class 3
CBSE Class 2
CBSE Class 1

Competitive Examinations

UPSC
NEET
JEE
CLAT
CAT
GMAT
GATE
Railways
SSC
IIT JAM
Defence
Insurance
Teaching
CA Foundation

Technical Exams

GATE
SSC JE
RRB JE
Civil Engineering
Computer Science Engineering
Electrical Engineering
Electronics Engineering
Biotechnology Engineering
Mechanical Engineering
Chemical Engineering

Important Questions for Circles- 2

Find all the important questions for Circles- 2 at EduRev.Get fully prepared for Circles- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Circles- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Circles- 2 resources.

Circles- 2 MCQs with Answers

Prepare for the Circles- 2 within the Grade 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Circles- 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Circles- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution