Sample Test: LR & DI- 1 - CAT MCQ
20 Questions MCQ Test - Sample Test: LR & DI- 1
Directions: Read the given information carefully and answer the question that follows.
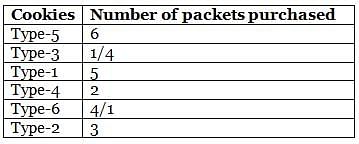
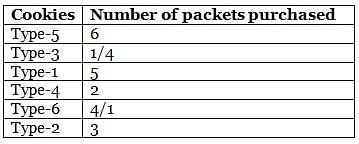
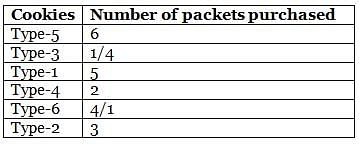
Amelia bought six different types (Type-1 to Type-6) of cookie packets from a bakery for her birthday party, each at a different price. The quantity of no two types of cookies bought by her is the same. Further, the quantity of each cookie packet that she bought is a natural number. She bought 5 packets of Type-1 and 3 packets of Type-2 cookies. The price of Type-3 cookies is more than that of Type-4 cookies, but less than that of Type-5 cookies. She bought a total of 21 packets of cookies, of which 6 packets were of the costliest type. Type-1 cookies are cheaper than Type-3 cookies, while Type-6 cookies are cheaper than Type-4 cookies, of which she bought 2 packets. Type-1 cookies are costlier than at least two types of cookies. Type-6 cookies are not the cheapest type of cookies that she bought.
Q. How many packets of the cheapest type of cookies did Amelia buy?
Directions: Read the given information carefully and answer the question that follows.
Amelia bought six different types (Type-1 to Type-6) of cookie packets from a bakery for her birthday party, each at a different price. The quantity of no two types of cookies bought by her is the same. Further, the quantity of each cookie packet that she bought is a natural number. She bought 5 packets of Type-1 and 3 packets of Type-2 cookies. The price of Type-3 cookies is more than that of Type-4 cookies, but less than that of Type-5 cookies. She bought a total of 21 packets of cookies, of which 6 packets were of the costliest type. Type-1 cookies are cheaper than Type-3 cookies, while Type-6 cookies are cheaper than Type-4 cookies, of which she bought 2 packets. Type-1 cookies are costlier than at least two types of cookies. Type-6 cookies are not the cheapest type of cookies that she bought.
Q. If Amelia bought 5 packets of the third cheapest type of cookies, then what is the third costliest type of cookies?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Read the given information carefully and answer the question that follows.
Amelia bought six different types (Type-1 to Type-6) of cookie packets from a bakery for her birthday party, each at a different price. The quantity of no two types of cookies bought by her is the same. Further, the quantity of each cookie packet that she bought is a natural number. She bought 5 packets of Type-1 and 3 packets of Type-2 cookies. The price of Type-3 cookies is more than that of Type-4 cookies, but less than that of Type-5 cookies. She bought a total of 21 packets of cookies, of which 6 packets were of the costliest type. Type-1 cookies are cheaper than Type-3 cookies, while Type-6 cookies are cheaper than Type-4 cookies, of which she bought 2 packets. Type-1 cookies are costlier than at least two types of cookies. Type-6 cookies are not the cheapest type of cookies that she bought.
Q. Which of the following statements is definitely false?
Directions: Read the given information carefully and answer the question that follows.
Amelia bought six different types (Type-1 to Type-6) of cookie packets from a bakery for her birthday party, each at a different price. The quantity of no two types of cookies bought by her is the same. Further, the quantity of each cookie packet that she bought is a natural number. She bought 5 packets of Type-1 and 3 packets of Type-2 cookies. The price of Type-3 cookies is more than that of Type-4 cookies, but less than that of Type-5 cookies. She bought a total of 21 packets of cookies, of which 6 packets were of the costliest type. Type-1 cookies are cheaper than Type-3 cookies, while Type-6 cookies are cheaper than Type-4 cookies, of which she bought 2 packets. Type-1 cookies are costlier than at least two types of cookies. Type-6 cookies are not the cheapest type of cookies that she bought.
Q. The maximum amount of money that Amelia spent was on
Directions: Read the given information carefully and answer the question that follows.
Amelia bought six different types (Type-1 to Type-6) of cookie packets from a bakery for her birthday party, each at a different price. The quantity of no two types of cookies bought by her is the same. Further, the quantity of each cookie packet that she bought is a natural number. She bought 5 packets of Type-1 and 3 packets of Type-2 cookies. The price of Type-3 cookies is more than that of Type-4 cookies, but less than that of Type-5 cookies. She bought a total of 21 packets of cookies, of which 6 packets were of the costliest type. Type-1 cookies are cheaper than Type-3 cookies, while Type-6 cookies are cheaper than Type-4 cookies, of which she bought 2 packets. Type-1 cookies are costlier than at least two types of cookies. Type-6 cookies are not the cheapest type of cookies that she bought.
Q. If Amelia spent the same amount of money on purchasing Type-2 and Type-6 cookies, how many packets of the second costliest cookies did she buy?
Directions: Study the following information and answer the question that follows.
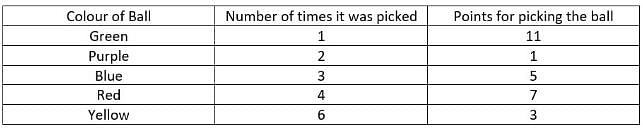
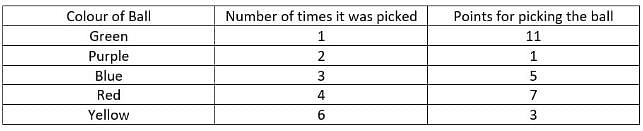
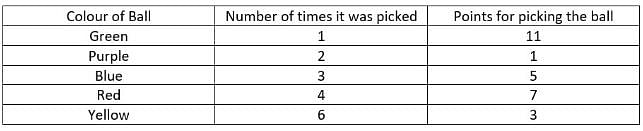
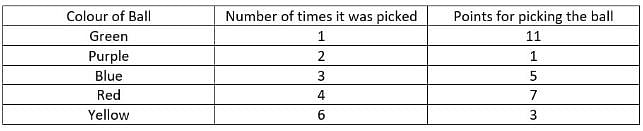
Four friends P, Q, R and S were playing a game in which they had to randomly pick a ball out of five balls of five different colours from a bag. They played the game for four rounds. The balls were of Red, Blue, Yellow, Green and Purple colours. Whenever they picked a ball, they got points 1, 3, 5, 7 and 11 for picking Purple, Yellow, Blue, Red and Green balls, respectively.
Further, the following information is known:
i. Each one of them picked different balls in each round except the last.
ii. Purple ball was picked more times than Green ball but less times than Blue ball.
iii. Each ball was picked at least once.
iv. R picked the ball which was picked only in round 2.
v. Red ball was picked in all the rounds and Q picked it in the second round.
vi. P, R and S picked different balls in all the four rounds.
vii. Total points earned because of Yellow ball were 18.
viii. P picked a Yellow ball in Round 2.
Q. Who picked a Purple ball in round 3?
Directions: Study the following information and answer the question that follows.
Four friends P, Q, R and S were playing a game in which they had to randomly pick a ball out of five balls of five different colours from a bag. They played the game for four rounds. The balls were of Red, Blue, Yellow, Green and Purple colours. Whenever they picked a ball, they got points 1, 3, 5, 7 and 11 for picking Purple, Yellow, Blue, Red and Green balls, respectively.
Further, the following information is known:
i. Each one of them picked different balls in each round except the last.
ii. Purple ball was picked more times than Green ball but less times than Blue ball.
iii. Each ball was picked at least once.
iv. R picked the ball which was picked only in round 2.
v. Red ball was picked in all the rounds and Q picked it in the second round.
vi. P, R and S picked different balls in all the four rounds.
vii. Total points earned because of Yellow ball were 18.
viii. P picked a Yellow ball in Round 2.
Q. Winner is the person scoring the highest points at the end of all the rounds. Who is the winner?
Directions: Study the following information and answer the question that follows.
Four friends P, Q, R and S were playing a game in which they had to randomly pick a ball out of five balls of five different colours from a bag. They played the game for four rounds. The balls were of Red, Blue, Yellow, Green and Purple colours. Whenever they picked a ball, they got points 1, 3, 5, 7 and 11 for picking Purple, Yellow, Blue, Red and Green balls, respectively.
Further, the following information is known:
i. Each one of them picked different balls in each round except the last.
ii. Purple ball was picked more times than Green ball but less times than Blue ball.
iii. Each ball was picked at least once.
iv. R picked the ball which was picked only in round 2.
v. Red ball was picked in all the rounds and Q picked it in the second round.
vi. P, R and S picked different balls in all the four rounds.
vii. Total points earned because of Yellow ball were 18.
viii. P picked a Yellow ball in Round 2.
Q. How many more minimum conditions are required to find who picked what in all the rounds?
Directions: Study the following information and answer the question that follows.
Four friends P, Q, R and S were playing a game in which they had to randomly pick a ball out of five balls of five different colours from a bag. They played the game for four rounds. The balls were of Red, Blue, Yellow, Green and Purple colours. Whenever they picked a ball, they got points 1, 3, 5, 7 and 11 for picking Purple, Yellow, Blue, Red and Green balls, respectively.
Further, the following information is known:
i. Each one of them picked different balls in each round except the last.
ii. Purple ball was picked more times than Green ball but less times than Blue ball.
iii. Each ball was picked at least once.
iv. R picked the ball which was picked only in round 2.
v. Red ball was picked in all the rounds and Q picked it in the second round.
vi. P, R and S picked different balls in all the four rounds.
vii. Total points earned because of Yellow ball were 18.
viii. P picked a Yellow ball in Round 2.
Q. If points scored by R in round 3 were 5, what was the colour of the ball picked by S in round 1?
Directions: Read the following passage and answer the question.
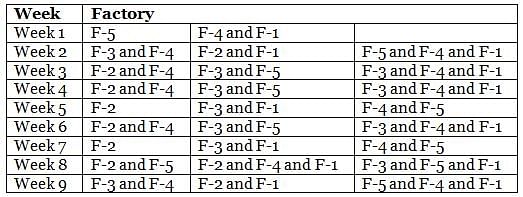
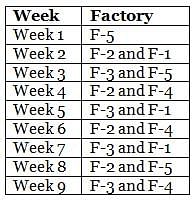
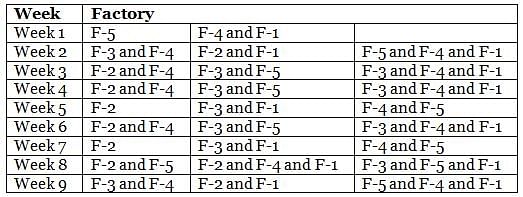
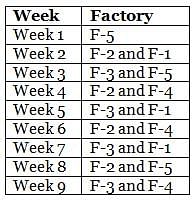
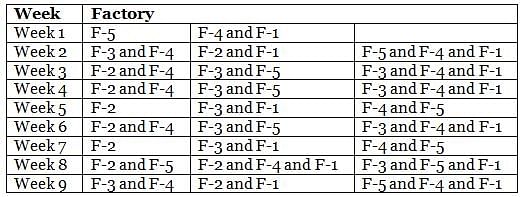
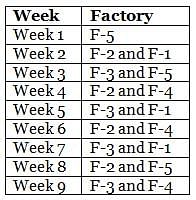
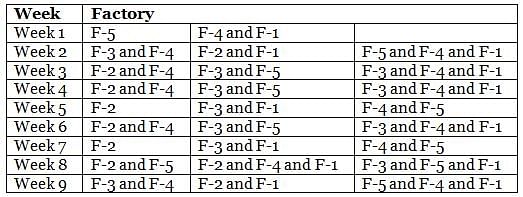
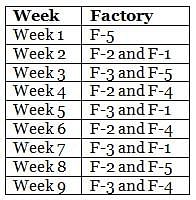
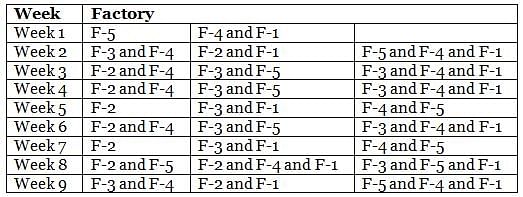
Mr. Joshua, owner of a group of industries, has five factories - Factory-1 to Factory-5. The distance that he travels in any week depends on the factory that he goes to during the week. In the weeks that he goes to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, he travels a distance longer than when he does not go to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, in any week in which case he travels exactly 30 km in that week. However, during the week, if he goes to Factory-1, he travels an additional 10 km; if he goes to Factory-4, he travels an additional 20 km; if he goes to Factory-5, he travels an additional 30 km; if he goes to Factory-3, he travels an additional 40 km; if he goes to Factory-2, he travels an additional 50 km. In any week, if he goes to more than one of the five types of factories mentioned above, he travels the additional distances corresponding to all the types of factories that he goes to in that week. He does not travel more after he goes to his factories in a particular week.
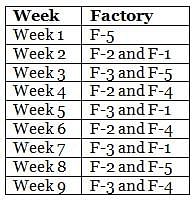
The table below provides the distance that Mr. Joshua travelled for nine weeks, from Week 1 through Week 9. Further, it is known that he did not travel to the same type of factory in any two consecutive weeks during the nine weeks.
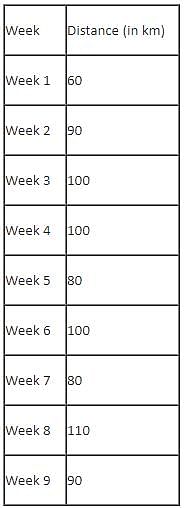
Q. During the nine weeks, for how many pairs of consecutive weeks did Mr. Joshua go to Factory-2 in the first week and Factory-5 in the next week?
Directions: Read the following passage and answer the question.
Mr. Joshua, owner of a group of industries, has five factories - Factory-1 to Factory-5. The distance that he travels in any week depends on the factory that he goes to during the week. In the weeks that he goes to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, he travels a distance longer than when he does not go to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, in any week in which case he travels exactly 30 km in that week. However, during the week, if he goes to Factory-1, he travels an additional 10 km; if he goes to Factory-4, he travels an additional 20 km; if he goes to Factory-5, he travels an additional 30 km; if he goes to Factory-3, he travels an additional 40 km; if he goes to Factory-2, he travels an additional 50 km. In any week, if he goes to more than one of the five types of factories mentioned above, he travels the additional distances corresponding to all the types of factories that he goes to in that week. He does not travel more after he goes to his factories in a particular week.
The table below provides the distance that Mr. Joshua travelled for nine weeks, from Week 1 through Week 9. Further, it is known that he did not travel to the same type of factory in any two consecutive weeks during the nine weeks.
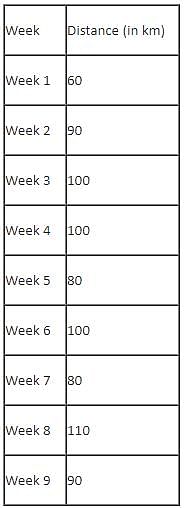
Q. In which of the following weeks did Mr. Joshua go to Factory-1?
Directions: Read the following passage and answer the question.
Mr. Joshua, owner of a group of industries, has five factories - Factory-1 to Factory-5. The distance that he travels in any week depends on the factory that he goes to during the week. In the weeks that he goes to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, he travels a distance longer than when he does not go to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, in any week in which case he travels exactly 30 km in that week. However, during the week, if he goes to Factory-1, he travels an additional 10 km; if he goes to Factory-4, he travels an additional 20 km; if he goes to Factory-5, he travels an additional 30 km; if he goes to Factory-3, he travels an additional 40 km; if he goes to Factory-2, he travels an additional 50 km. In any week, if he goes to more than one of the five types of factories mentioned above, he travels the additional distances corresponding to all the types of factories that he goes to in that week. He does not travel more after he goes to his factories in a particular week.
The table below provides the distance that Mr. Joshua travelled for nine weeks, from Week 1 through Week 9. Further, it is known that he did not travel to the same type of factory in any two consecutive weeks during the nine weeks.
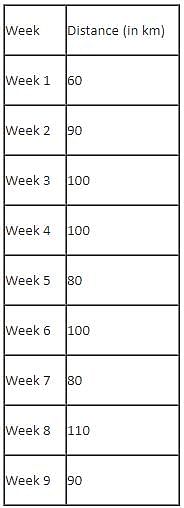
Q. Which of the following factories did Mr. Joshua go to in the maximum number of weeks during the given period?
Directions: Read the following passage and answer the question.
Mr. Joshua, owner of a group of industries, has five factories - Factory-1 to Factory-5. The distance that he travels in any week depends on the factory that he goes to during the week. In the weeks that he goes to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, he travels a distance longer than when he does not go to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, in any week in which case he travels exactly 30 km in that week. However, during the week, if he goes to Factory-1, he travels an additional 10 km; if he goes to Factory-4, he travels an additional 20 km; if he goes to Factory-5, he travels an additional 30 km; if he goes to Factory-3, he travels an additional 40 km; if he goes to Factory-2, he travels an additional 50 km. In any week, if he goes to more than one of the five types of factories mentioned above, he travels the additional distances corresponding to all the types of factories that he goes to in that week. He does not travel more after he goes to his factories in a particular week.
The table below provides the distance that Mr. Joshua travelled for nine weeks, from Week 1 through Week 9. Further, it is known that he did not travel to the same type of factory in any two consecutive weeks during the nine weeks.

Q. In how many of the nine weeks did Mr. Joshua go to Factory-3 but not to Factory-5?
Directions: Read the following passage and answer the question.
Mr. Joshua, owner of a group of industries, has five factories - Factory-1 to Factory-5. The distance that he travels in any week depends on the factory that he goes to during the week. In the weeks that he goes to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, he travels a distance longer than when he does not go to Factory-1 or Factory-2 or Factory-3 or Factory-4 or Factory-5, in any week in which case he travels exactly 30 km in that week. However, during the week, if he goes to Factory-1, he travels an additional 10 km; if he goes to Factory-4, he travels an additional 20 km; if he goes to Factory-5, he travels an additional 30 km; if he goes to Factory-3, he travels an additional 40 km; if he goes to Factory-2, he travels an additional 50 km. In any week, if he goes to more than one of the five types of factories mentioned above, he travels the additional distances corresponding to all the types of factories that he goes to in that week. He does not travel more after he goes to his factories in a particular week.
The table below provides the distance that Mr. Joshua travelled for nine weeks, from Week 1 through Week 9. Further, it is known that he did not travel to the same type of factory in any two consecutive weeks during the nine weeks.
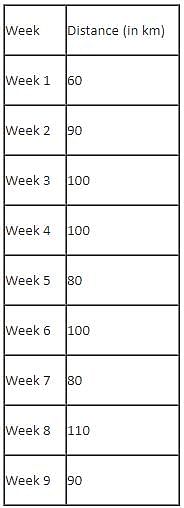
Q. Which factories were visited by Mr. Joshua in the week immediately preceded by the one which witnessed his visit to the same factories as the one that immediately succeeded that week?
Directions: Answer the given question based on the following data:
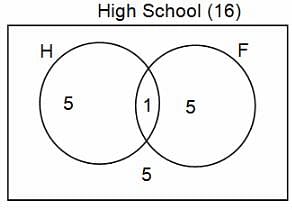
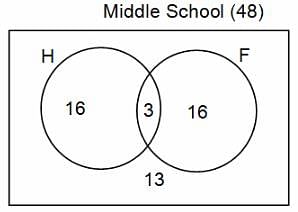
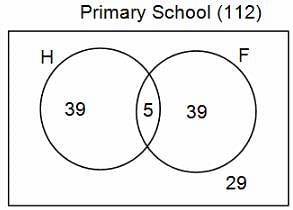
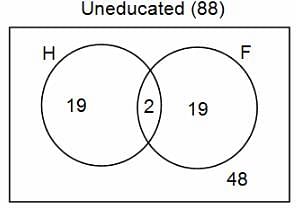
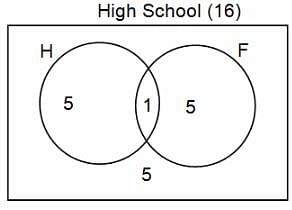
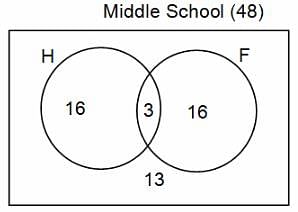
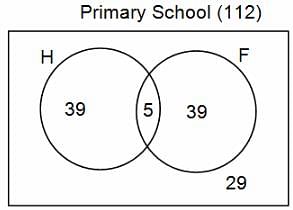
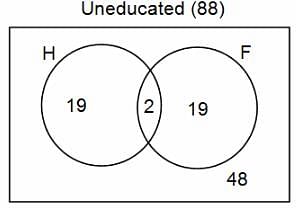
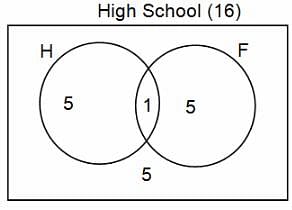
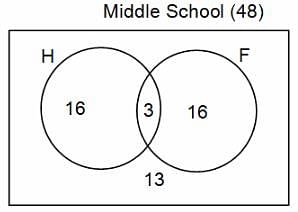
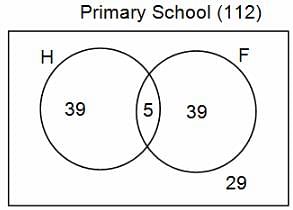
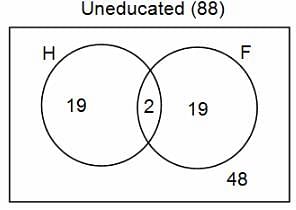
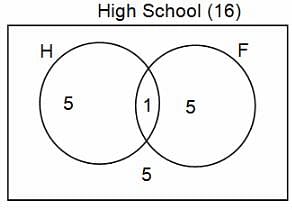
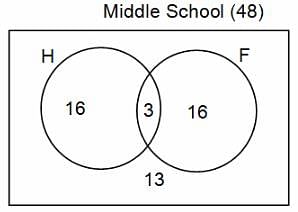
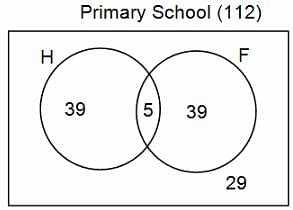
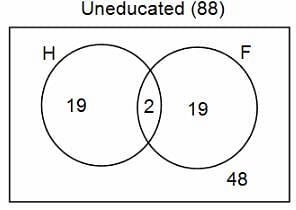
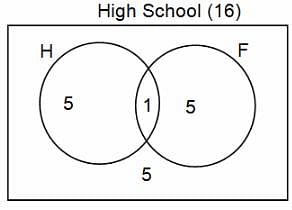
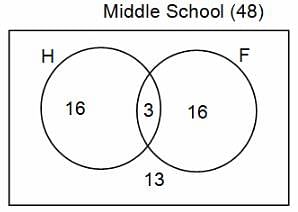
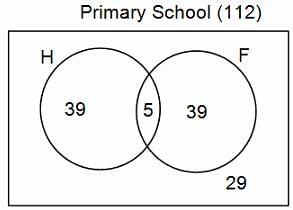
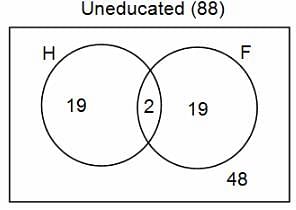
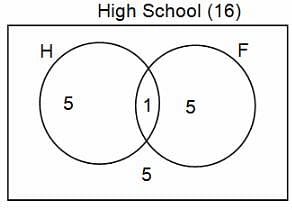
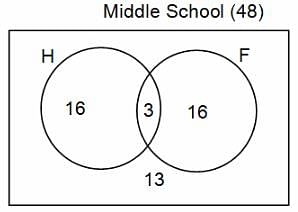
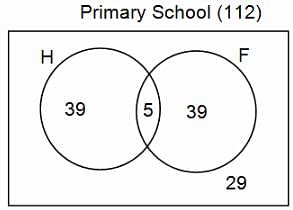
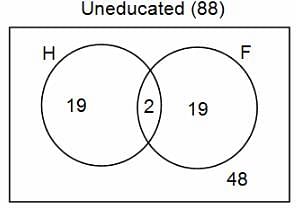
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many people have middle school education?
Directions: Answer the given question based on the following data:
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many people have middle school education?
Directions: Answer the given question based on the following data:
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many people having middle school education, but not high school education, play only football?
Directions: Answer the given question based on the following data:
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many people who completed primary school could not finish middle school?
Directions: Answer the given question based on the following data:
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many uneducated people play neither hockey nor football?
Directions: Answer the given question based on the following data:
In a group of 200 people, number of people having at least primary education : number of people having at least middle school education: number of people having at least high school education are in the ratio 7 : 3 : 1. Out of these, 90 play football and 60 play hockey. Also, 5 in Category III (people having high school education) and one-fourth each in Categories I and II (people having primary school education only and people having middle school education but not high school education, respectively) do not play any game. In each of the above categories, the number of people who play only hockey equals the number of people who play only football. Two persons each in Categories I and II and one person in Category III play both the games. Two persons who play both the games are uneducated (Category IV). Five persons in Category III play only hockey.
Assume middle school education can be had only after completing primary school and high school education can be had only after completing middle school. Also all people in the group fall under one of the four categories described above.
Q. How many persons are there who play atleast one game?