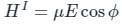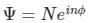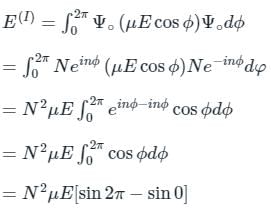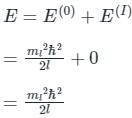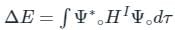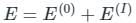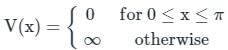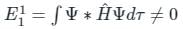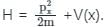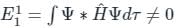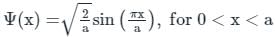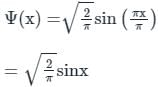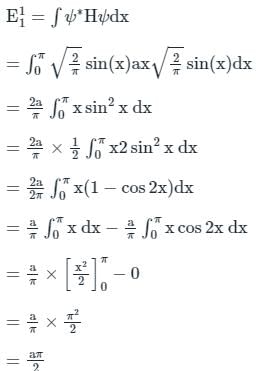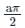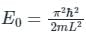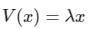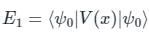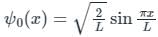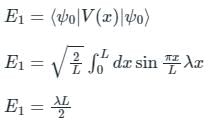Test: Perturbation Theory - GATE Physics MCQ
10 Questions MCQ Test - Test: Perturbation Theory
The unperturbed energy levels of a system are ε2 = 0, ε2= 2 and ε2 = 4. The second order correction to energy for the ground state in pressure of the perturbation V for which V10 = 2, V20 = 4, and V12 = 6 has been found to be
A perturbation Ĥ' = V0(3 cos2ϕ – 1), where V0 is a constant, is applied to a rigid rotator undergoing a rotational motion in a plane. The first order energy correction to the ground state is
The perturbation,

acts on a particle of mass m confined in an infinite square well potential

The first order to the ground state energy will be

acts on a particle of mass m confined in an infinite square well potential

The first order to the ground state energy will be
When a hydrogen atom is exposed to a perturbation V = E.z, the first order correction to the wave function comes only from the orbital
The first-order correction to energy for the ground state of a particle-in-a-box of length a  would be
would be
A perturbation of the form  is added in a 1-D box having length 0 to L. The total energy of the system corrected up to first order is;
is added in a 1-D box having length 0 to L. The total energy of the system corrected up to first order is;
An electron in a hydrogen atom is exposed to a perturbation V = V0rCos φ. The first order correction to the ground-state energy of the electron is
Consider a particle on a ring that is perturbed by interacting with an applied electric field (E) with the perturbation being H' = μE cos Φ, where μ is the dipole moment. The energy levels correct upto first order are
If the perturbation H' = ax, where a is a constant, is added to an infinite square well potential
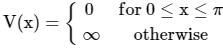
The correction to the ground state energy to first order in a is
The first-order correction to energy for the ground state of a particle-in-a-box due to a perturbation λx would be


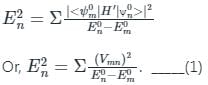
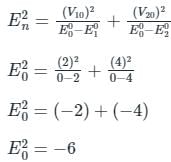
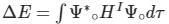
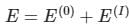
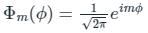

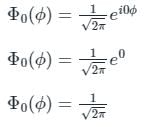
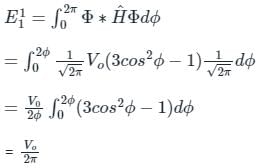
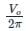

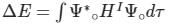
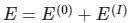
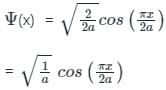
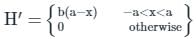
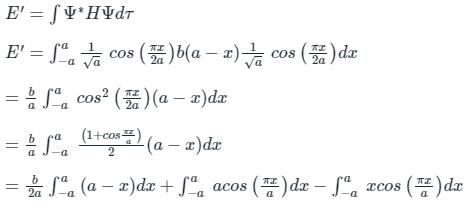
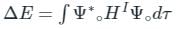
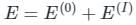
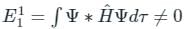
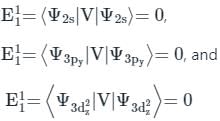
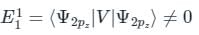

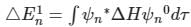 (First-order Energy correction)
(First-order Energy correction)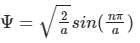
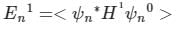
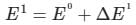
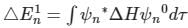 (First-order Energy correction)
(First-order Energy correction)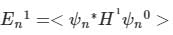
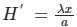
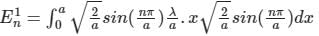
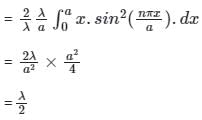

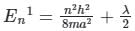
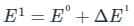
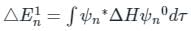 (First-order Energy correction)
(First-order Energy correction)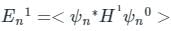
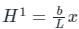
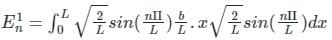
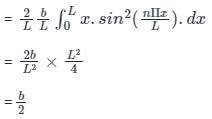
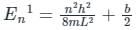
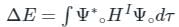
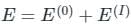
 where ml is the magnetic quantum number.
where ml is the magnetic quantum number.