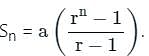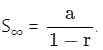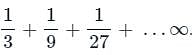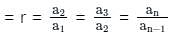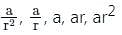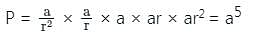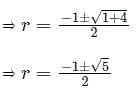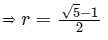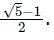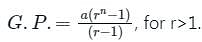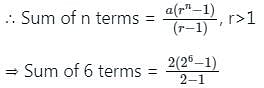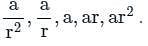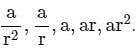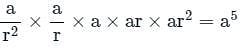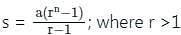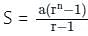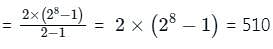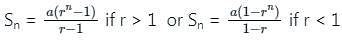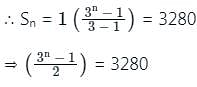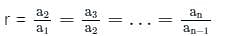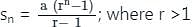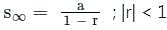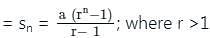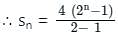MCQ: Geometric Progressions - 3 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Geometric Progressions - 3
If the 4th, 7th and 10th terms of a G.P. be a, b, c respectively, then the relation between a, b, c is
If 21/e, 2b/ac, 21/a are in GP, then which one of the following is correct ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a G.P , the 5th term is 96 and 8th term is 768 , then the 3rd term of G.P is ?
If the sum of n numbers in the GP 5, 10, 20, ... is 1275 then n is ?
In a G.P. of positive terms , if every term is equal to the sum of next two terms. Then find the common ratio of the G.P.
The third term of a GP is 3. What is the product of its first five terms?
What is the nth term of the sequence 25, -125, 625, -3125, …….?
The terms of a G.P. are positive. If each term is equal to the sum of two terms that follows it, then the common ratio is
If nth term of a G.P. is 2n then find the sum of its first 6 terms.
The third term of a G.P. is 9. The product of its first five terms is
For what possible value of x are the numbers - 2/7, x, - 7/2 are in a GP ?
A man has 2 parents, 4 grandparents, 8 great- grand parents, and so on . Find the number of ancestors during the 8 generations preceding his own .
For the series 1 + 3 + 32 + ... , the sum to n terms is 3280. Find the value of n.
If the sum of n numbers in the GP 4, 8, 16, ... is 2044 then n is ?


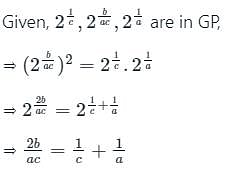
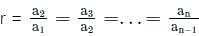
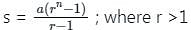
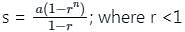
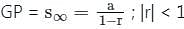
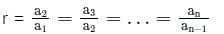
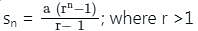
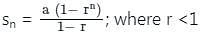
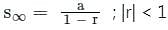
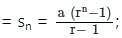 where r >1
where r >1
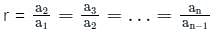

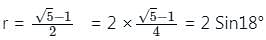
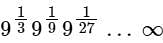 is:
is: